Spirolateral

Simple spirolaterals
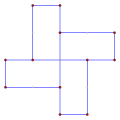
3_90° (4 cycles)	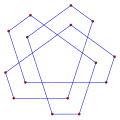3_108° (5 cycles)	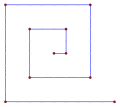9_90° ccw spiral	9_90° (4 cycles)
100_120° spiral		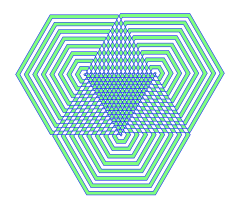100_120° (4 cycles)

In Euclidean geometry, a spirolateral is a polygon created by a sequence of fixed vertex internal angles and sequential edge lengths 1,2,3,...,n which repeat until the figure closes. The number of repeats needed is called its cycles.^[1] A simple spirolateral has only positive angles. A simple spiral approximates of a portion of an archimedean spiral. A general spirolateral allows positive and negative angles.

A spirolateral which completes in one turn is a simple polygon, while requiring more than 1 turn is a star polygon and must be self-crossing.^[2] A simple spirolateral can be an equangular simple polygon <p> with p vertices, or an equiangular star polygon <p/q> with p vertices and q turns.

Spirolaterals were invented and named by Frank C. Odds as a teenager in 1962, as square spirolaterals with 90° angles, drawn on graph paper. In 1970, Odds discovered triangular and hexagonal spirolateral, with 60° and 120° angles, can be drawn on isometric^[3] (triangular) graph paper.^[4] Odds wrote to Martin Gardner who encouraged him to publish the results in Mathematics Teacher^[5] in 1973.^[3]

The process can be represented in turtle graphics, alternating turn angle and move forward instructions, but limiting the turn to a fixed rational angle.^[2]

The smallest golygon is a spirolateral, 7_90°⁴, made with 7 right angles, and length 4 follow concave turns. Golygons are different in that they must close with a single sequence 1,2,3,..n, while a spirolateral will repeat that sequence until it closes.

Classifications

Varied cases
Simple 6_90°, 2 cycle, 3 turn	Regular unexpected closed spirolateral, 8_90°^1,5	Unexpectedly closed spirolateral 7_90°⁴	Crossed rectangle (1,2,-1,-2)_60°
Crossed hexagon (1,1,2,-1,-1,-2)_90°	(-1.2.4.3.2)_60°	(2...4)_90°	(2,1,-2,3,-4,3)_120°

A simple spirolateral has turns all the same direction.^[2] It is denoted by n_θ, where n is the number of sequential integer edge lengths and θ is the internal angle, as any rational divisor of 360°. Sequential edge lengths can be expressed explicitly as (1,2,...,n)_θ.

Note: The angle θ can be confusing because it represents the internal angle, while the supplementary turn angle can make more sense. These two angles are the same for 90°.

This defines an equiangular polygon of the form <kp/kq>, where angle θ = 180(1−2q/p), with k = n/d, and d = gcd(n,p). If d = n, the pattern never closes. Otherwise it has kp vertices and kq density. The cyclic symmetry of a simple spirolateral is p/d-fold.

A regular polygon, {p} is a special case of a spirolateral, 1_{180(1−2/p)°}. A regular star polygon, {p/q}, is a special case of a spirolateral, 1_{180(1−2q/p)°}. An isogonal polygon, is a special case spirolateral, 2_{180(1−2/p)°} or 2_{180(1−2q/p)°}.

A general spirolateral can turn left or right.^[2] It is denoted by n_θ^a₁,...,a_k, where a_i are indices with negative or concave angles.^[6] For example, 2_60°² is a crossed rectangle with ±60° internal angles, bending left or right.

An unexpected closed spirolateral returns to the first vertex on a single cycle. Only general spirolaterals may not close. A golygon is a regular unexpected closed spirolateral that closes from the expected direction. An irregular unexpected closed spirolateral is one that returns to the first point but from the wrong direction. For example 7_90°⁴. It takes 4 cycles to return to the start in the correct direction.^[2]

A modern spirolateral, also called a loop-de-loops^[7] by Educator Anna Weltman, is denoted by (i₁,...,i_n)_θ, allowing any sequence of integers as the edge lengths, i₁ to i_n.^[8] For example, (2,3,4)_90° has edge lengths 2,3,4 repeating. Opposite direction turns can be given a negative integer edge length. For example, a crossed rectangle can be given as (1,2,−1,−2)_θ.

An open spirolateral never closes. A simple spirolateral, n_θ, never closes if nθ is a multiple of 360°, gcd(p,n) = p. A general spirolateral can also be open if half of the angles are positive, half negative.

A (partial) infinite simple spirolateral, 4_90°

Closure

The number of cycles it takes to close a spirolateral, n_θ, with k opposite turns can be computed like so. Define p and q such that p/q=360/(180-θ). if the fraction (p-2q)(n-2k)/2p is reduced fully to a/b, then the figure repeats after b cycles, and complete a total turns. If b=1, the figure never closes.^[1]

Explicitly, the number of cycles is 2p/d, where d=gcd((p-2q)(n-2k),2p). If d=2p, it closes on 1 cycle or never.

The number of cycles can be seen as the rotational symmetry order of the spirolateral.

n_90°

1_90°, 4 cycle, 1 turn
2_90°, 2 cycle, 1 turn
3_90°, 4 cycle, 3 turn
4_90°, never closes
5_90°, 4 cycle, 5 turn
6_90°, 2 cycle, 3 turn
7_90°, 4 cycle, 6 turns
8_90°, never closes
9_90°, 4 cycle, 9 turn
10_90°, 2 cycle, 5 turn

n_60°

1_60°, 3 cycle, 1 turn
2_60°, 3 cycle, 2 turn
3_60°, never closes
4_60°, 3 cycle, 4 turn
5_60°, 3 cycle, 5 turn
6_60°, never closes
7_60°, 3 cycle, 7 turn
8_60°, 3 cycle, 8 turn
9_60°, never closes
10_60°, 3 cycle, 10 turn

Small simple spirolaterals

Spirolaterals can be constructed from any rational divisor of 360°. The first table's columns sample angles from small regular polygons and second table from star polygons, with examples up to n = 6.

An equiangular polygon <p/q> has p vertices and q density. <np/nq> can be reduced by d = gcd(n,p).

Small whole divisor angles

Simple spirolaterals (whole divisors p) n_θ or (1,2,...,n)_θ
θ	60°	90°	108°	120°	128 4/7°	135°	140°	144°	147 3/11°	150°
180-θ Turn angle	120°	90°	72°	60°	51 3/7°	45°	40°	36°	32 8/11°	30°
n_θ \ p	3	4	5	6	7	8	9	10	11	12
1_θ Regular {p}	1_60° {3}	1_90° {4}	1_108° {5}	1_120° {6}	1_128.57° {7}	1_135° {8}	1_140° {9}	1_144° {10}	1_147.27° {11}	1_150° {12}
2_θ Isogonal <2p/2>	2_60° <6/2>	2_90° <8/2> → <4>	2_108° <10/2>	2_120° <12/2> → <6>	2_128.57° <14/2>	2_135° <16/2> → <8>	2_140° <18/2>	2_144° <20/2> → <10>	2_147° <22/2>	2_150° <24/2> → <12>
3_θ 2-isogonal <3p/3>	3_60° open	3_90° <12/3>	3_108° <15/3>	3_120° <18/3> → <6>	3_128.57° <21/3>	3_135° <24/3>	3_140° <27/3> → <9>	3_144° <30/3>	3_147° <33/3>	3_150° <36/3> → <12>
4_θ 3-isogonal <4p/4>	4_60° <12/4>	4_90° open	4_108° <20/4>	4_120° <24/4> → <12/2>	4_128.57° <28/4>	4_135° <32/4> → <8>	4_140° <36/4>	4_144° <40/4> → <20/2>	4_147° <44/4>	4_150° <48/4> → <12>
5_θ 4-isogonal <5p/5>	5_60° <15/5>	5_90° <20/5>	5_108° open	5_120° <30/5>	5_128.57° <35/5>	5_135° <40/5>	5_140° <45/5>	5_144° <50/5> → <10>	5_147° <55/5>	5_150° <60/5>
6_θ 5-isogonal <6p/6>	6_60° Open	6_90° <24/6> → <12/3>	6_108° <30/6>	6_120° Open	6_128.57° <42/6>	6_135° <48/6> → <24/3>	6_140° <54/6> → <18/2>	6_144° <60/6> → <30/3>	6_147° <66/6>	6_150° <72/6> → <12>

Small rational divisor angles

Simple spirolaterals (rational divisors p/q) n_θ or (1,2,...,n)_θ
θ	15°	16 4/11°	20°	25 5/7°	30°	36°	45°	49 1/11°	72°	77 1/7°	81 9/11°	100°	114 6/11°
180-θ Turn angle	165°	163 7/11°	160°	154 2/7°	150°	144°	135°	130 10/11°	108°	102 6/7°	98 2/11°	80°	65 5/11°
n_θ \ p/q	24/11	11/5	9/4	7/3	12/5	5/2	8/3	11/4	10/3	7/2	11/3	9/2	11/2
1_θ Regular {p/q}	1_15° {24/11}	1_16.36° {11/5}	1_20° {9/4}	1_25.71° {7/3}	1_30° {12/5}	1_36° {5/2}	1_45° {8/3}	1_49.10° {11/4}	1_72° {10/3}	1_77.14° {7/2}	1_81.82° {11/3}	1_100° {9/2}	1_114.55° {11/2}
2_θ Isogonal <2p/2q>	2_15° <48/22> → <24/11>	2_16.36° <22/10>	2_20° <18/8>	2_25.71° <14/6>	2_30° <24/10> → <12/5>	2_36° <10/4>	2_45° <16/6> → <8/3>	2_49.10° <22/8>	2_72° <20/6> → <10/3>	2_77.14° <14/4>	2_81.82° <22/6>	2_100° <18/4>	2_114.55° <22/4>
3_θ 2-isogonal <3p/3q>	3_15° <72/33> → <24/11>	3_16.36° <33/15>	3_20° <27/12> → <9/4>	3_25.71° <21/9>	3_30° <36/15> → <12/5>	3_36° <15/6>	3_45° <24/9>	3_49.10° <33/12>	3_72° <30/9>	3_77.14° <21/6>	3_81.82° <33/9>	3_100° <27/6> → <9/2>	3_114.55° <33/6>
4_θ 3-isogonal <4p/4q>	4_15° <96/44> → <24/11>	4_16.36° <44/20>	4_20° <36/12>	4_25.71° <28/4>	4_30° <48/40> → <12/5>	4_36° <20/8>	4_45° <32/12> → <8/3>	4_49.10° <44/16>	4_72° <40/12> → <20/6>	4_77.14° <28/8>	4_81.82° <44/12>	4_100° <36/8>	4_114.55° <44/8>
5_θ 4-isogonal <5p/5q>	5_15° <120/55>	5_16.36° <55/25>	5_20° <45/20>	5_25.71° <35/15>	5_30° <60/25>	5_36° open	5_45° <40/15>	5_49.10° <55/20>	5_72° <50/15> → <10/3>	5_77.14° <35/10>	5_81.82° <55/15>	5_100° <45/10>	5_114.55° <55/10>
6_θ 5-isogonal <6p/6q>	6_15° <144/66> → <24/11>	6_16.36° <66/30>	6_20° <54/24> → <18/8>	6_25.71° <42/18>	6_30° <72/30> → <12/5>	6_36° <30/12>	6_45° <48/18> → <24/9>	6_49.10° <66/24>	6_72° <60/18> → <30/9>	6_77.14° <42/12>	6_81.82° <66/18>	6_100° <54/12> → <18/4>	6_114.55° <66/12>

References

^ ^a ^b Gardner, M. Worm Paths Ch. 17 Knotted Doughnuts and Other Mathematical Entertainments New York: W. H. Freeman, pp. 205-221, 1986. [1]
^ ^a ^b ^c ^d ^e Abelson, Harold, diSessa, Andera, 1980, Turtle Geometry, MIT Press, pp.37-39, 120-122
^ ^a ^b Focus on...Spirolaterals Secondary Magazine Issue 78
^ [2] Frank Odds, British biochemist, 8/29/1945-7/7/2020
^ Odds, Frank C. Spirolaterals, Mathematics Teacher, Feb 1973, Volume 66: Issue 2, pp. 121–124 DOI
^ Weisstein, Eric W. "Spirolateral". MathWorld.
^ Anna Weltman, This is Not a Math Book A Graphic Activity Book, Kane Miller; Act Csm edition, 2017
^ "Practice Multiplication with Simple Spirolateral Math Art". 23 July 2015.

Alice Kaseberg Schwandt Spirolaterals: An advanced Investignation from an Elementary Standpoint, Mathematical Teacher, Vol 72, 1979, 166-169 [3]
Margaret Kenney and Stanley Bezuszka, Square Spirolaterals Mathematics Teaching, Vol 95, 1981, pp. 22–27 [4]
Gascoigne, Serafim Turtle Fun LOGO for the Spectrum 48K pp 42-46 | Spirolaterals 1985
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry London: Penguin, pp. 239–241, 1991.
Krawczyk, Robert, "Hilbert's Building Blocks", Mathematics & Design, The University of the Basque Country, pp. 281–288, 1998.
Krawczyk, Robert, Spirolaterals, Complexity from Simplicity, International Society of Arts, Mathematics and Architecture 99, The University of the Basque Country, pp. 293–299, 1999. [5]
Krawczyk, Robert J. The Art of Spirolateral reversals [6]

External links

Spirolaterals Javascript App

[gardner-1] Gardner, M. Worm Paths Ch. 17 Knotted Doughnuts and Other Mathematical Entertainments New York: W. H. Freeman, pp. 205-221, 1986. [1]

[turtle-2] Abelson, Harold, diSessa, Andera, 1980, Turtle Geometry, MIT Press, pp.37-39, 120-122

[focus-3] Focus on...Spirolaterals Secondary Magazine Issue 78

[4] [2] Frank Odds, British biochemist, 8/29/1945-7/7/2020

[5] Odds, Frank C. Spirolaterals, Mathematics Teacher, Feb 1973, Volume 66: Issue 2, pp. 121–124 DOI

[6] Weisstein, Eric W. "Spirolateral". MathWorld.

[7] Anna Weltman, This is Not a Math Book A Graphic Activity Book, Kane Miller; Act Csm edition, 2017

[8] "Practice Multiplication with Simple Spirolateral Math Art". 23 July 2015.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]