Resonant inelastic X-ray scattering (RIXS) is an advanced X-ray spectroscopy technique.[1][2]
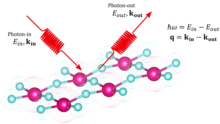
In the last two decades RIXS has been widely exploited to study the electronic, magnetic and structural properties of quantum materials and molecules. It is a resonant X-rays photon-in photon-out energy loss and momentum resolved spectroscopy, capable of measuring the energy and momentum transferred to specific excitations proper of the sample under study.[1][2]
The use of X-rays guarantees bulk sensitivity, as opposed to electron spectroscopies, and the tuning of the incoming X-rays to a specific absorption edge allows for element and chemical specificity.[1][2][3]
Due to the intrinsic inefficiency of the RIXS process, extremely brilliant sources of X-rays are crucial. In addition to that, the possibility to tune the energy of the incoming X-rays is compelling to match a chosen resonance. These two strict conditions make RIXS to be necessarily performed at synchrotrons or nowadays at X-ray free electron lasers (XFELs) and set the advent of third generation synchrotrons (1994, ESRF[4]) as a turning point for the success of the technique.[1][2]
Exploiting different experimental setups, RIXS can be performed using both soft and hard X-rays, spanning a vast range of absorption edges and thus samples to be studied.[1]
RIXS process
editRIXS is a two steps process. First an electron is resonantly excited from a core level, defined by the absorption edge, to an empty state, leaving a core hole. The intermediate state with the core hole has a lifetime of few femtoseconds, then the system radiatively decays into the final state with the filling of the core hole and the emission of another photon. Since the probability of a radiative core hole relaxation is low, the RIXS cross section is very small and a high brilliance X-ray source is needed. Being a second order process, the RIXS cross section is described by the Kramers-Heisenberg formula.[1][5]
The scattering geometry (incidence and scattering angles) determines the momentum transfer . In order to explore the space the spectrometer angle with respect to the incoming beam can be changed, as well as the incident angle to the sample.[1][5]
The RIXS process can be classified as either direct or indirect. This distinction is useful because the cross-sections for each are quite different. When direct scattering is allowed, it will be the dominant scattering channel, with indirect processes contributing only in higher order. In contrast, for the large class of experiments for which direct scattering is forbidden, RIXS relies exclusively on indirect scattering channels.[1][5]
Direct RIXS
editIn direct RIXS, the incoming photon promotes a core-electron to an empty valence band state. Subsequently, an electron from a different state decays and annihilates the core-hole. The hole in the final state may either be in a core level at lower binding energy than in the intermediate state or in the filled valence shell. Some authors refer to this technique as resonant X-ray emission spectroscopy (RXES). The distinction between RIXS, resonant X-ray Raman and RXES in the literature is not strict.[2]
The net result is a final state with an electron-hole excitation, as an electron was created in an empty valence band state and a hole in a filled shell. If the hole is in the filled valence shell, the electron-hole excitation can propagate through the material, carrying away momentum and energy. Momentum and energy conservation require that these are equal to the momentum and energy loss of the scattered photon.[1]
For direct RIXS to occur, both photoelectric transitions—the initial one from core to valence state and succeeding one to fill the core hole—must be possible. These transitions can for instance be an initial dipolar transition of 1s → 2p followed by the decay of another electron in the 2p band from 2p → 1s. This happens at the K-edge of oxygen, carbon and silicon. Very efficient sequence often used in 3d transition metals are a 1s → 3d excitation followed by a 2p → 1s decay.[6]
Indirect RIXS
editIndirect RIXS is slightly more complicated. Here, the incoming photon promotes a core-electron to an itinerant state far above the electronic chemical potential. Subsequently, the electron in this same state decays again, filling the core-hole. Scattering of the X-rays occurs via the core-hole potential that is present in the intermediate state. It shakes up the electronic system, creating excitations to which the X-ray photon loses energy and momentum.[7][8][9] The number of electrons in the valence sub-system is constant throughout the process.[5][10][11]
Experimental details
editIn general the natural linewidth of a spectral feature is determined by the life-times of initial and final states. Indeed, as for X-ray absorption and non-resonant X-ray emission spectroscopy the energy resolution is often limited by the relatively short life-time of the final state core-hole. As in RIXS a high energy core-hole is absent in the final state, this leads to intrinsically sharp spectra with energy and momentum resolution determined by the instrumentation.[3][2][1][12]
A convolution of the incident X-ray bandpass, defined by the beamline monochromator, and the bandpass of the RIXS spectrometer for the analysis of the scattered photons energy gives the total (combined) energy resolution. Since RIXS exploits high energy photons in the X-ray range, a very large combined resolving power (103-105 depending on the goal of the experiment) is needed to detail the different spectral features. Therefore, in the last two decades efforts have been made to improve RIXS spectrometers performances, gaining orders of magnitude in terms of resolving power.[13] State of the art soft X-rays RIXS beamlines in use at the ESRF, at DLS and at NSLS II, have reached approximately 40000 of combined resolving power, leading to a record energy resolution of 25 meV at Cu L3 edge.[14][15][16]
As for hard X-rays, the optical design is different and requires the use of Bragg reflection crystal analyzers. Thus, the resolving power is mostly determined by the crystal analyzers in use.[17][18]
Soft X-ray spectrometers
editState of the art soft X-ray RIXS spectrometers are based on grazing incidence diffraction gratings, to disperse the X-rays scattered from the sample, and on position sensitive detectors, mostly CCDs. The two-dimensional image shows a vertical dispersive direction and a non-dispersive one. Integrating along the non-dispersive direction one can obtain a spectrum.[13][14][15][16][19]
The whole optical path from the source to the CCD must be kept in UHV to minimize the absorption of X-rays by air.[20] The number of optical elements is typically minimized, which is important for a number of reasons. Indeed, the low reflectivity of optical elements for X-rays reduces the throughput. In addition to that, a non-negligible contribution to the combined resolving power is due to the imperfections on the surface of mirrors and gratings (slope error). Finally, the lower the number of optical elements to be aligned, the better in terms of setup time.[13][14][15][16][19]
The monochromatized X-rays impinge on the sample with a defined geometry and are scattered and collected by the spectrometer. Collection mirrors are often placed after the sample, the distance (1 cm to 1 m) depends on the optical design. This is useful to increase the acceptance angle of the spectrometer and thus the efficiency.[13][14][15][16]
After the collecting optics X-rays are dispersed by the varied line spacing (VLS) grating that can be either plane or spherical. In the former case, a vertical focusing mirror is added to the optical path to focus the X-rays on the detector, in the latter the grating itself also focuses the dispersed X-rays on the CCD detector. Depending on the absorption edge chosen for the experiment, the respective positions between the grating and the detector, and the incidence angle of the grating can be tuned to optimize the spectrometer in a large energy window, without changing any optical element.[13][14][15][16]
Since the spectral analysis of the scattered X-rays is done through a dispersive grating, longer spectrometers offer higher resolving power. State of the art spectrometers are more than ten meters long, more than five times the dimensions of the pioneering ones. Two examples from ESRF and DLS are in the figures.[14][15][16]
Hard X-ray spectrometers
editThe optical layout for hard X-rays RIXS spectrometers is different. The spectrometers are based on spherical crystal analyzers (typically more than one to increase the solid angle of the spectrometer) exploiting Bragg reflections and on a position sensitive detector, typically in the so called Rowland geometry. This means that the source (X-rays spot on the sample), the analyzers and the detector must sit on the Rowland circle. By scanning the positions of the analyzers and of the detector (the source is fixed for convenience) the Bragg condition is changed and thus the energy of the scattered X-rays can be analyzed. By increasing the radius of the Rowland circle, the energy resolution can be increased, loosing in terms of efficiency. Nevertheless, as opposed to soft X-rays spectrometers, the resolving power of the spectrometer is limited by the crystal analyzers. Thus, increasing too much the dimensions of the spectrometer does not pay off.[18][22][23]
Depending on the chosen absorption edge (and thus incidence energy), different crystal analyzers are used both on the monochromator side and on the spectrometer side. Thanks to the high penetration depth of hard X-rays, there is no need of UHV. Therefore, the exchange of optical elements, such as crystal analyzers, is less disruptive than for soft X-rays.[17][18][22][23]
One of the major technical challenges in these RIXS experiments is selecting the monochromator and energy analyzer which produce, at the desired energy, the desired resolution. Some of the feasible crystal monochromator reflections and energy analyzer reflections have been tabulated.[24][25]
RIXS properties
editCompared to other inelastic scattering techniques as INS, IXS, EELS or Raman scattering that present shortcomings, RIXS has a number of unique features: it covers a large scattering phase-space thanks to the high energy photons, it is polarization dependent, element specific, bulk sensitive and requires only small sample volumes enabling studies on thin films as well as diluted solutions. RIXS is a resonant technique because the energy of the incident photon is chosen such that it coincides with, and hence resonates with, one of the atomic X-ray absorption edges of the system. The resonance greatly enhances the valence contribution to the inelastic scattering cross section, sometimes by many orders of magnitude.[3][2][1][26]
Comparing the energy of a neutron, electron or photon with a wavelength of the order of the relevant length scale in a solid - as given by the de Broglie equation considering the interatomic lattice spacing is in the order of Ångströms - it derives from the relativistic energy–momentum relation that an X-ray photon has more energy than a neutron or electron. The scattering phase space (the range of energies and momenta that can be transferred in a scattering event) of X-rays is therefore without equal. In particular, high-energy X-rays carry a momentum that is comparable to the inverse lattice spacing of typical condensed matter systems so that, unlike Raman scattering experiments with visible or infrared light, RIXS can probe the full dispersion of low energy excitations in solids.[1][2][3]
RIXS can utilize the polarization of the photon: the nature of the excitations created in the material can be disentangled by a polarization analysis of the incident and scattered photons, which allow one, through the use of various selection rules, to characterize the symmetry and nature of the excitations.[1][2][3]
RIXS is element specific: chemical sensitivity arises by tuning to the absorption edges of the different types of elements in a material. RIXS can even differentiate between the same chemical element at sites with different valencies or at inequivalent crystallographic positions as long as the X-ray absorption edges in these cases are distinguishable. In addition, the type of information on the electronic excitations of a system being probed can be varied by tuning to different X-ray edges (e.g., K, L or M) of the same chemical element, where the photon excites core-electrons into different valence orbitals.[1][2][3]
RIXS is bulk sensitive: the penetration depth of resonant X-ray photons depends on the material and on the scattering geometry, but typically is of the order of a few micrometers in the hard X-rays regime (for example at transition metal K-edges) and on the order of 0.1 micrometers in the soft X-ray regime (e.g. transition metal L-edges).[1][2][3]
RIXS needs only small sample volumes: the photon-matter interaction is relatively strong, compared to for instance to the neutron-matter interaction strength. This makes RIXS feasible on very small volume samples, thin films, surfaces and nano-objects, in addition to bulk single crystal, powder samples or diluted solutions.[1][2][3]
RIXS spectral features
editIn principle RIXS can probe a very broad class of intrinsic excitations of the system under study, as long as the excitations are overall charge neutral. This constraint arises from the fact that in RIXS the scattered photons do not add or remove charge from the sample.[1]
Starting from the low energy loss part of the spectrum, RIXS has a purely elastic response, which hosts both a diffused elastic signal, but also any kind of order proper of the system, as charge density waves.[1][27][28][29][30]
In the low-energy window, the signal is dominated by phonons and vibrational modes that are present in a RIXS spectrum through the electron-phonon coupling. Only a portion of phonons modes that characterize the sample are visible through RIXS.[1][31][32][33]
Electron-hole continuum and excitons in band metals, doped systems and semiconductors are visible through RIXS, thanks to the enhancement of valence charge excitations guaranteed by the resonance character of the technique.[1][34]
In the charge channel, also plasmons and their dispersion can be measured by RIXS,[1][35][36][37] as well as orbital and crystal field excitations[38][39] and charge transfer excitations.[1]
Spin excitations are symmetry-allowed in RIXS as well. In particular, RIXS at L and M edges, thanks to the resonant character, also spin flip excitations (magnons) can be accessed with RIXS, exploiting the spin-orbit coupling of the core level involved in the RIXS process. This makes RIXS as the paramount technique to study magnon dispersions, thanks to the higher cross-section with respect to INS. Besides magnons, RIXS can probe bi-magnons and spinons.[1][40][39][41]
Moreover, it has been theoretically shown that RIXS can probe Bogoliubov quasiparticles in high-temperature superconductors,[42] and shed light on the nature and symmetry of the electron-electron pairing of the superconducting state.[43]
Pump-probe RIXS with X-ray free electron lasers (XFELs)
editWith the advent of XFELs, sources that can provide extremely brilliant (more than five orders of magnitude larger than synchrotron sources) and extremely short X-ray pulses, X-ray spectroscopies performed in a pump and probe fashion are nowadays available.[44][45]
The power of pump-probe spectroscopies lies in the possibility to study how a system evolves after an external stimulus. The most straightforward example is the study of photoactivated biological process, such as the photosynthesis: the sample is illuminated by an optical laser tuned at the proper wavelength and then its evolution is observed taking snapshots as a function of time.[44][45]
The development of high-resolution RIXS spectrometers at XFELs is opening a new field, exploiting the power of RIXS to study the photo-induced transient states in quantum materials and photoactivated processes in molecules.[46][47][48][49][50]
Applications
edit- Intracellular metal speciation,[51]
- Mott insulators[7][9][8][52][53][54][55]
- high-temperature superconductors (e.g., cuprates),[39][55][56][57][58][59][60][61][62][63][64]
- Iron-based superconductors,[65]
- Semiconductors (e.g. Cu2O)[66][55]
- Colossal magnetoresistance manganites.[67]
- Metalloproteins (e.g. the oxygen-evolving complex in photosystem II)[6] aqueous myoglobins[68]
- Catalysis[69]
- Water,[70][71][72] aqueous solution,[73][74] aqueous acetic acid,[75] aqueous glycine[76]
- High pressure.[77][78]
See also
editReferences
edit- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z Ament, Luuk J. P.; van Veenendaal, Michel; Devereaux, Thomas P.; Hill, John P.; van den Brink, Jeroen (2011-06-24). "Resonant inelastic x-ray scattering studies of elementary excitations". Reviews of Modern Physics. 83 (2): 705–767. arXiv:1009.3630. doi:10.1103/RevModPhys.83.705.
- ^ a b c d e f g h i j k l de Groot, Frank; Kotani, Akio (2008-03-10). Core Level Spectroscopy of Solids. CRC Press. pp. 335–435. doi:10.1201/9781420008425. ISBN 978-0-429-19579-2.
- ^ a b c d e f g h Schülke, W. (2007). Electron dynamics by inelastic X-ray scattering (1st ed.). Oxford university press. pp. 377–479. ISBN 978-0-19-851017-8.
- ^ Raimondi, Pantaleo (2016). "ESRF-EBS: The Extremely Brilliant Source Project". Synchrotron Radiation News. 29 (6): 8–15. doi:10.1080/08940886.2016.1244462. ISSN 0894-0886.
- ^ a b c d Brink, J. van den; Veenendaal, M. van (2006). "Correlation functions measured by indirect resonant inelastic X-ray scattering". Europhysics Letters (EPL). 73 (1). IOP Publishing: 121–127. Bibcode:2006EL.....73..121V. doi:10.1209/epl/i2005-10366-9. ISSN 0295-5075. S2CID 250849541.
- ^ a b Glatzel, Pieter; Bergmann, Uwe; Yano, Junko; Visser, Hendrik; Robblee, John H.; et al. (2004). "The Electronic Structure of Mn in Oxides, Coordination Complexes, and the Oxygen-Evolving Complex of Photosystem II Studied by Resonant Inelastic X-ray Scattering". Journal of the American Chemical Society. 126 (32). American Chemical Society (ACS): 9946–9959. doi:10.1021/ja038579z. ISSN 0002-7863. PMC 3960404. PMID 15303869.
- ^ a b Hasan, M. Z.; Isaacs, E. D.; Shen, Z.-X.; Miller, L. L.; Tsutsui, K.; Tohyama, T.; Maekawa, S. (2000-06-09). "Electronic Structure of Mott Insulators Studied by Inelastic X-ray Scattering". Science. 288 (5472): 1811–1814. arXiv:cond-mat/0102489. Bibcode:2000Sci...288.1811H. doi:10.1126/science.288.5472.1811. ISSN 0036-8075. PMID 10846160. S2CID 2581764.
- ^ a b Hasan, M. Z.; Isaacs, E. D.; Shen, Z. -X.; Miller, L. L. (2001-03-01). "Inelastic X-ray scattering as a novel tool to study electronic excitations in complex insulators". Journal of Electron Spectroscopy and Related Phenomena. Proceeding of the Eight International Conference on Electronic Spectroscopy and Structure. 114–116: 705–709. doi:10.1016/S0368-2048(00)00401-1. ISSN 0368-2048.
- ^ a b Hasan, M. Z.; Isaacs, E. D.; Shen, Z-X.; Miller, L. L. (2000-11-01). "Particle-hole excitations in insulating antiferromagnet Ca2CuO2Cl2". Physica C: Superconductivity. 341–348: 781–782. Bibcode:2000PhyC..341..781H. doi:10.1016/S0921-4534(00)00690-0. ISSN 0921-4534.
- ^ Hancock, J N; Chabot-Couture, G; Greven, M (2010-03-03). "Lattice coupling and Franck–Condon effects in K-edge resonant inelastic x-ray scattering". New Journal of Physics. 12 (3). IOP Publishing: 033001. arXiv:1004.0859. Bibcode:2010NJPh...12c3001H. doi:10.1088/1367-2630/12/3/033001. ISSN 1367-2630. S2CID 118673022.
- ^ Vernay, F.; Moritz, B.; Elfimov, I. S.; Geck, J.; Hawthorn, D.; Devereaux, T. P.; Sawatzky, G. A. (2008-03-18). "CuK-edge resonant inelastic x-ray scattering in edge-sharing cuprates". Physical Review B. 77 (10): 104519. arXiv:cond-mat/0702026. Bibcode:2008PhRvB..77j4519V. doi:10.1103/physrevb.77.104519. ISSN 1098-0121. S2CID 119045219.
- ^ Glatzel, P.; Sikora, M.; Fernández-García, M. (2009). "Resonant X-ray spectroscopy to study K absorption pre-edges in 3d transition metal compounds". The European Physical Journal Special Topics. 169 (1). Springer Science and Business Media LLC: 207–214. Bibcode:2009EPJST.169..207G. doi:10.1140/epjst/e2009-00994-7. ISSN 1951-6355. S2CID 121110109.
- ^ a b c d e f Ghiringhelli, G.; Piazzalunga, A.; Dallera, C.; Trezzi, G.; Braicovich, L.; Schmitt, T.; Strocov, V. N.; Betemps, R.; Patthey, L.; Wang, X.; Grioni, M. (2006-11-01). "SAXES, a high resolution spectrometer for resonant x-ray emission in the 400–1600eV energy range". Review of Scientific Instruments. 77 (11). doi:10.1063/1.2372731. ISSN 0034-6748.
- ^ a b c d e f Brookes, N. B.; Yakhou-Harris, F.; Kummer, K.; Fondacaro, A.; Cezar, J. C.; Betto, D.; Velez-Fort, E.; Amorese, A.; Ghiringhelli, G.; Braicovich, L.; Barrett, R.; Berruyer, G.; Cianciosi, F.; Eybert, L.; Marion, P. (2018-09-21). "The beamline ID32 at the ESRF for soft X-ray high energy resolution resonant inelastic X-ray scattering and polarisation dependent X-ray absorption spectroscopy". Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 903: 175–192. doi:10.1016/j.nima.2018.07.001. hdl:11311/1128322. ISSN 0168-9002.
- ^ a b c d e f Zhou, K.-J.; Walters, A.; Garcia-Fernandez, M.; Rice, T.; Hand, M.; Nag, A.; Li, J.; Agrestini, S.; Garland, P.; Wang, H.; Alcock, S.; Nistea, I.; Nutter, B.; Rubies, N.; Knap, G. (2022-03-01). "I21: an advanced high-resolution resonant inelastic X-ray scattering beamline at Diamond Light Source". Journal of Synchrotron Radiation. 29 (2): 563–580. doi:10.1107/S1600577522000601. ISSN 1600-5775. PMC 8900866. PMID 35254322.
- ^ a b c d e f Dvorak, Joseph; Jarrige, Ignace; Bisogni, Valentina; Coburn, Scott; Leonhardt, William (2016-11-01). "Towards 10 meV resolution: The design of an ultrahigh resolution soft X-ray RIXS spectrometer". Review of Scientific Instruments. 87 (11). doi:10.1063/1.4964847. ISSN 0034-6748.
- ^ a b Gog, T.; Casa, D. M.; Knopp, J.; Kim, J.; Upton, M. H.; Krakora, R.; Jaski, A.; Said, A.; Yavaş, H.; Gretarsson, H.; Huang, X. R. (2018-07-01). "Performance of quartz- and sapphire-based double-crystal high-resolution (∼10 meV) RIXS monochromators under varying power loads". Journal of Synchrotron Radiation. 25 (4): 1030–1035. doi:10.1107/S1600577518005945. ISSN 1600-5775.
- ^ a b c Moretti Sala, M.; Martel, K.; Henriquet, C.; Al Zein, A.; Simonelli, L.; Sahle, C.; Gonzalez, H.; Lagier, M.-C.; Ponchut, C.; Huotari, S.; Verbeni, R.; Krisch, M.; Monaco, G. (2018-03-01). "A high-energy-resolution resonant inelastic X-ray scattering spectrometer at ID20 of the European Synchrotron Radiation Facility". Journal of Synchrotron Radiation. 25 (2): 580–591. doi:10.1107/S1600577518001200. hdl:11311/1049071. ISSN 1600-5775.
- ^ a b Dinardo, M. E.; Piazzalunga, A.; Braicovich, L.; Bisogni, V.; Dallera, C.; Giarda, K.; Marcon, M.; Tagliaferri, A.; Ghiringhelli, G. (2007-01-01). "Gaining efficiency and resolution in soft X-ray emission spectrometers thanks to directly illuminated CCD detectors". Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 570 (1): 176–181. doi:10.1016/j.nima.2006.10.024. ISSN 0168-9002.
- ^ "Physics.nist.gov". Physics.nist.gov. Retrieved 2023-07-06.
- ^ Gao, Xing; Gu, Songqi; Gao, Qian; Zou, Yang; Jiang, Zheng; Zhang, Shuo; Wei, Xiangjun; Yu, Haisheng; Sheng, Guodong; Duan, Peiquan; Huang, Yuying (2013). "A high-resolution X-ray fluorescence spectrometer and its application at SSRF: A high-resolution X-ray fluorescence spectrometer and its application". X-Ray Spectrometry. 42 (6): 502–507. doi:10.1002/xrs.2511.
- ^ a b Huotari, S.; Albergamo, F.; Vankò, Gy.; Verbeni, R.; Monaco, G. (2006). "Resonant inelastic hard x-ray scattering with diced analyzer crystals and position-sensitive detectors". Review of Scientific Instruments. 77 (5). doi:10.1063/1.2198805.
- ^ a b Moretti Sala, M.; Henriquet, C.; Simonelli, L.; Verbeni, R.; Monaco, G. (2013-06-01). "High energy-resolution set-up for Ir L3 edge RIXS experiments". Journal of Electron Spectroscopy and Related Phenomena. Progress in Resonant Inelastic X-Ray Scattering. 188: 150–154. doi:10.1016/j.elspec.2012.08.002. ISSN 0368-2048.
- ^ ["Archived copy". Archived from the original on 2013-02-09. Retrieved 2012-06-06.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ "Archived copy". Archived from the original on 2013-02-09. Retrieved 2012-06-06.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Barbiellini, Bernardo; Hancock, Jason N.; Monney, Claude; Joly, Yves; Ghiringhelli, Giacomo; Braicovich, Lucio; Schmitt, Thorsten (2014-06-30). "Inelastic x-ray scattering from valence electrons near absorption edges of FeTe and TiSe2". Physical Review B. 89 (23): 235138. arXiv:1009.3630. Bibcode:2014PhRvB..89w5138B. doi:10.1103/PhysRevB.89.235138. S2CID 119231739.
- ^ Ghiringhelli, G.; Le Tacon, M.; Minola, M.; Blanco-Canosa, S.; Mazzoli, C.; Brookes, N. B.; De Luca, G. M.; Frano, A.; Hawthorn, D. G.; He, F.; Loew, T.; Sala, M. Moretti; Peets, D. C.; Salluzzo, M.; Schierle, E. (2012-08-17). "Long-Range Incommensurate Charge Fluctuations in (Y,Nd)Ba 2 Cu 3 O 6+ x". Science. 337 (6096): 821–825. arXiv:1207.0915. doi:10.1126/science.1223532. ISSN 0036-8075.
- ^ Arpaia, R.; Caprara, S.; Fumagalli, R.; De Vecchi, G.; Peng, Y. Y.; Andersson, E.; Betto, D.; De Luca, G. M.; Brookes, N. B.; Lombardi, F.; Salluzzo, M.; Braicovich, L.; Di Castro, C.; Grilli, M.; Ghiringhelli, G. (2019-08-30). "Dynamical charge density fluctuations pervading the phase diagram of a Cu-based high-Tc superconductor". Science. 365 (6456): 906–910. arXiv:1809.04949. doi:10.1126/science.aav1315. ISSN 0036-8075.
- ^ Comin, Riccardo; Damascelli, Andrea (2016-03-10). "Resonant X-Ray Scattering Studies of Charge Order in Cuprates". Annual Review of Condensed Matter Physics. 7 (1): 369–405. arXiv:1509.03313. doi:10.1146/annurev-conmatphys-031115-011401. ISSN 1947-5454.
- ^ Arpaia, Riccardo; Ghiringhelli, Giacomo (2021-11-15). "Charge Order at High Temperature in Cuprate Superconductors". Journal of the Physical Society of Japan. 90 (11): 111005. arXiv:2106.00731. doi:10.7566/jpsj.90.111005. ISSN 0031-9015.
- ^ Devereaux, T. P.; Shvaika, A. M.; Wu, K.; Wohlfeld, K.; Jia, C. J.; Wang, Y.; Moritz, B.; Chaix, L.; Lee, W.-S.; Shen, Z.-X.; Ghiringhelli, G.; Braicovich, L. (2016-10-25). "Directly Characterizing the Relative Strength and Momentum Dependence of Electron-Phonon Coupling Using Resonant Inelastic X-Ray Scattering". Physical Review X. 6 (4): 041019. arXiv:1605.03129. doi:10.1103/physrevx.6.041019. ISSN 2160-3308.
- ^ Rossi, Matteo; Arpaia, Riccardo; Fumagalli, Roberto; Moretti Sala, Marco; Betto, Davide; Kummer, Kurt; De Luca, Gabriella M.; van den Brink, Jeroen; Salluzzo, Marco; Brookes, Nicholas B.; Braicovich, Lucio; Ghiringhelli, Giacomo (2019-07-08). "Experimental Determination of Momentum-Resolved Electron-Phonon Coupling". Physical Review Letters. 123 (2): 027001. arXiv:1902.09163. doi:10.1103/physrevlett.123.027001. ISSN 0031-9007.
- ^ Braicovich, Lucio (2016), "High Resolution Resonant Inelastic X-Ray Scattering from Solids in the Soft Range", Synchrotron Light Sources and Free-Electron Lasers, Cham: Springer International Publishing, pp. 1797–1822, doi:10.1007/978-3-319-14394-1_42, ISBN 978-3-319-14393-4, retrieved 2023-07-06
- ^ Jia, Chunjing; Wohlfeld, Krzysztof; Wang, Yao; Moritz, Brian; Devereaux, Thomas P. (2016-05-13). "Using RIXS to Uncover Elementary Charge and Spin Excitations". Physical Review X. 6 (2): 021020. arXiv:1510.05068. doi:10.1103/physrevx.6.021020. ISSN 2160-3308.
- ^ Nag, Abhishek; Zhu, M.; Bejas, Matías; Li, J.; Robarts, H. C.; Yamase, Hiroyuki; Petsch, A. N.; Song, D.; Eisaki, H.; Walters, A. C.; García-Fernández, M.; Greco, Andrés; Hayden, S. M.; Zhou, Ke-Jin (2020-12-14). "Detection of Acoustic Plasmons in Hole-Doped Lanthanum and Bismuth Cuprate Superconductors Using Resonant Inelastic X-Ray Scattering". Physical Review Letters. 125 (25): 257002. doi:10.1103/physrevlett.125.257002. hdl:1983/4135a219-e672-4666-a98d-94d300a4287b. ISSN 0031-9007.
- ^ Hepting, M.; Bejas, M.; Nag, A.; Yamase, H.; Coppola, N.; Betto, D.; Falter, C.; Garcia-Fernandez, M.; Agrestini, S.; Zhou, Ke-Jin; Minola, M.; Sacco, C.; Maritato, L.; Orgiani, P.; Wei, H. I. (2022-07-19). "Gapped Collective Charge Excitations and Interlayer Hopping in Cuprate Superconductors". Physical Review Letters. 129 (4): 047001. arXiv:2206.14083. doi:10.1103/physrevlett.129.047001. ISSN 0031-9007.
- ^ Vojta, Matthias; Vojta, Thomas; Kaul, Ribhu K. (2006-08-28). "Spin Excitations in Fluctuating Stripe Phases of Doped Cuprate Superconductors". Physical Review Letters. 97 (9): 097001. arXiv:cond-mat/0510448. doi:10.1103/physrevlett.97.097001. ISSN 0031-9007.
- ^ Moretti Sala, M; Bisogni, V; Aruta, C; Balestrino, G; Berger, H; Brookes, N B; Luca, G M de; Di Castro, D; Grioni, M; Guarise, M; Medaglia, P G; Miletto Granozio, F; Minola, M; Perna, P; Radovic, M (2011-04-19). "Energy and symmetry of dd excitations in undoped layered cuprates measured by CuL3resonant inelastic x-ray scattering". New Journal of Physics. 13 (4): 043026. arXiv:1009.4882. doi:10.1088/1367-2630/13/4/043026. ISSN 1367-2630.
- ^ a b c Schlappa, J.; Wohlfeld, K.; Zhou, K. J.; Mourigal, M.; Haverkort, M. W.; et al. (2012-04-18). "Spin–orbital separation in the quasi-one-dimensional Mott insulator Sr2CuO3". Nature. 485 (7396). Springer Science and Business Media LLC: 82–85. arXiv:1205.1954. Bibcode:2012Natur.485...82S. doi:10.1038/nature10974. ISSN 0028-0836. PMID 22522933. S2CID 43990784.
- ^ Braicovich, L.; van den Brink, J.; Bisogni, V.; Sala, M. Moretti; Ament, L. J. P.; Brookes, N. B.; De Luca, G. M.; Salluzzo, M.; Schmitt, T.; Strocov, V. N.; Ghiringhelli, G. (2010-02-19). "Magnetic Excitations and Phase Separation in the Underdoped La 2− x Sr x CuO 4 Superconductor Measured by Resonant Inelastic X-Ray Scattering". Physical Review Letters. 104 (7): 077002. doi:10.1103/physrevlett.104.077002. ISSN 0031-9007.
- ^ Martinelli, Leonardo; Betto, Davide; Kummer, Kurt; Arpaia, Riccardo; Braicovich, Lucio; Di Castro, Daniele; Brookes, Nicholas B.; Moretti Sala, Marco; Ghiringhelli, Giacomo (2022-05-19). "Fractional Spin Excitations in the Infinite-Layer Cuprate CaCuO2". Physical Review X. 12 (2): 021041. arXiv:2110.06666. doi:10.1103/physrevx.12.021041. ISSN 2160-3308.
- ^ Marra, Pasquale; Sykora, Steffen; Wohlfeld, Krzysztof; van den Brink, Jeroen (2013). "Resonant Inelastic X-Ray Scattering as a Probe of the Phase and Excitations of the Order Parameter of Superconductors". Physical Review Letters. 110 (11): 117005. arXiv:1212.0112. Bibcode:2013PhRvL.110k7005M. doi:10.1103/PhysRevLett.110.117005. ISSN 0031-9007. PMID 25166567. S2CID 21978160.
- ^ Marra, Pasquale; van den Brink, Jeroen; Sykora, Steffen (2016-05-06). "Theoretical approach to resonant inelastic x-ray scattering in iron-based superconductors at the energy scale of the superconducting gap". Scientific Reports. 6 (1): 25386. arXiv:1405.5556. Bibcode:2016NatSR...625386M. doi:10.1038/srep25386. ISSN 2045-2322. PMC 4858731. PMID 27151253.
- ^ a b Willmott, Philip (2019). An Introduction to Synchrotron Radiation. Wiley. pp. 107–126. doi:10.1002/9781119280453. ISBN 978-1-119-28039-2.
- ^ a b Decking, W.; Abeghyan, S.; Abramian, P.; Abramsky, A.; Aguirre, A.; Albrecht, C.; Alou, P.; Altarelli, M.; Altmann, P.; Amyan, K.; Anashin, V.; Apostolov, E.; Appel, K.; Auguste, D.; Ayvazyan, V. (2020). "A MHz-repetition-rate hard X-ray free-electron laser driven by a superconducting linear accelerator". Nature Photonics. 14 (6): 391–397. doi:10.1038/s41566-020-0607-z. ISSN 1749-4893.
- ^ Dean, M. P. M.; Cao, Y.; Liu, X.; Wall, S.; Zhu, D.; Mankowsky, R.; Thampy, V.; Chen, X. M.; Vale, J. G.; Casa, D.; Kim, Jungho; Said, A. H.; Juhas, P.; Alonso-Mori, R.; Glownia, J. M.; Robert, A.; Robinson, J.; Sikorski, M.; Song, S.; Kozina, M.; Lemke, H.; Patthey, L.; Owada, S.; Katayama, T.; Yabashi, M.; Tanaka, Yoshikazu; Togashi, T.; Liu, J.; Rayan Serrao, C.; Kim, B. J.; Huber, L.; Chang, C.-L.; McMorrow, D. F.; Först, M.; Hill, J. P. (June 2016). "Ultrafast energy- and momentum-resolved dynamics of magnetic correlations in the photo-doped Mott insulator Sr2IrO4". Nature Materials. 15 (6): 601–605. arXiv:1604.02439. doi:10.1038/nmat4641.
- ^ Mazzone, Daniel G.; Meyers, Derek; Cao, Yue; Vale, James G.; Dashwood, Cameron D.; Shi, Youguo; James, Andrew J. A.; Robinson, Neil J.; Lin, Jiaqi; Thampy, Vivek; Tanaka, Yoshikazu; Johnson, Allan S.; Miao, Hu; Wang, Ruitang; Assefa, Tadesse A.; Kim, Jungho; Casa, Diego; Mankowsky, Roman; Zhu, Diling; Alonso-Mori, Roberto; Song, Sanghoon; Yavas, Hasan; Katayama, Tetsuo; Yabashi, Makina; Kubota, Yuya; Owada, Shigeki; Liu, Jian; Yang, Junji; Konik, Robert M.; Robinson, Ian K.; Hill, John P.; McMorrow, Desmond F.; Först, Michael; Wall, Simon; Liu, Xuerong; Dean, Mark P. M. (June 2021). "Laser-induced transient magnons in Sr 3 Ir 2 O 7 throughout the Brillouin zone". Proceedings of the National Academy of Sciences. 118 (22): e2103696118. doi:10.1073/pnas.2103696118. PMC 8179144. PMID 34039712.
- ^ Chen, Yuan; Wang, Yao; Jia, Chunjing; Moritz, Brian; Shvaika, Andrij M.; Freericks, James K.; Devereaux, Thomas P. (2019-03-22). "Theory for time-resolved resonant inelastic x-ray scattering". Physical Review B. 99 (10): 104306. arXiv:1901.11255. doi:10.1103/physrevb.99.104306. ISSN 2469-9950.
- ^ Mitrano, Matteo; Wang, Yao (2020-10-19). "Probing light-driven quantum materials with ultrafast resonant inelastic X-ray scattering". Communications Physics. 3 (1). arXiv:2009.11315. doi:10.1038/s42005-020-00447-6. ISSN 2399-3650.
- ^ Mitrano, Matteo; Lee, Sangjun; Husain, Ali A.; Delacretaz, Luca; Zhu, Minhui; de la Peña Munoz, Gilberto; Sun, Stella X.-L.; Joe, Young Il; Reid, Alexander H.; Wandel, Scott F.; Coslovich, Giacomo; Schlotter, William; van Driel, Tim; Schneeloch, John; Gu, G. D. (2019-08-02). "Ultrafast time-resolved x-ray scattering reveals diffusive charge order dynamics in La2-xBaxCuO4". Science Advances. 5 (8): eaax3346. doi:10.1126/sciadv.aax3346. ISSN 2375-2548. PMC 6697434. PMID 31453340.
- ^ Stewart, Theodora J. (2017). "Chapter 5. Lead Speciation in Microorganisms". In Astrid, S.; Helmut, S.; Sigel, R. K. O. (eds.). Lead: Its Effects on Environment and Health. Metal Ions in Life Sciences. Vol. 17. de Gruyter. pp. 79–98. doi:10.1515/9783110434330-005. PMID 28731298.
- ^ Hasan, M. Z.; Montano, P. A.; Isaacs, E. D.; Shen, Z.-X.; Eisaki, H.; Sinha, S. K.; Islam, Z.; Motoyama, N.; Uchida, S. (2002-04-16). "Momentum-Resolved Charge Excitations in a Prototype One-Dimensional Mott Insulator". Physical Review Letters. 88 (17): 177403. arXiv:cond-mat/0102485. Bibcode:2002PhRvL..88q7403H. doi:10.1103/PhysRevLett.88.177403. PMID 12005784. S2CID 30809135.
- ^ Hasan, M. Z.; Chuang, Y.-D.; Li, Y.; Montano, P.; Beno, M.; Hussain, Z.; Eisaki, H.; Uchida, S.; Gog, T.; Casa, D. M. (2003-08-10). "Direct Spectroscopic Evidence of Holons in a Quantum Antiferromagnetic Spin-1/2 Chain". International Journal of Modern Physics B. 17 (18n20): 3479–3483. Bibcode:2003IJMPB..17.3479H. doi:10.1142/S0217979203021241. ISSN 0217-9792.
- ^ Wray, L.; Qian, D.; Hsieh, D.; Xia, Y.; Eisaki, H.; Hasan, M. Z. (2007-09-19). "Dispersive collective charge modes in an incommensurately modulated cuprate Mott insulator". Physical Review B. 76 (10): 100507. arXiv:cond-mat/0612207. Bibcode:2007PhRvB..76j0507W. doi:10.1103/PhysRevB.76.100507. S2CID 119333385.
- ^ a b c Markiewicz, R. S.; Hasan, M. Z.; Bansil, A. (2008-03-25). "Acoustic plasmons and doping evolution of Mott physics in resonant inelastic x-ray scattering from cuprate superconductors". Physical Review B. 77 (9): 094518. Bibcode:2008PhRvB..77i4518M. doi:10.1103/PhysRevB.77.094518.
- ^ Kotani, A.; Okada, K.; Vankó, György; Dhalenne, G.; Revcolevschi, A.; Giura, P.; Shukla, Abhay (2008-05-20). "Cu Kαresonant x-ray emission spectroscopy of high-Tc-related cuprates". Physical Review B. 77 (20). American Physical Society (APS): 205116. Bibcode:2008PhRvB..77t5116K. doi:10.1103/physrevb.77.205116. ISSN 1098-0121.
- ^ Braicovich, L.; Ament, L. J. P.; Bisogni, V.; Forte, F.; Aruta, C.; et al. (2009-04-20). "Dispersion of Magnetic Excitations in the Cuprate La2CuO4 and CaCuO2 Compounds Measured Using Resonant X-Ray Scattering". Physical Review Letters. 102 (16). American Physical Society (APS): 167401. Bibcode:2009PhRvL.102p7401B. doi:10.1103/physrevlett.102.167401. hdl:2066/75508. ISSN 0031-9007. PMID 19518752. S2CID 2543028.
- ^ Le Tacon, M.; Ghiringhelli, G.; Chaloupka, J.; Sala, M. Moretti; Hinkov, V.; et al. (2011-07-10). "Intense paramagnon excitations in a large family of high-temperature superconductors". Nature Physics. 7 (9): 725–730. arXiv:1106.2641. Bibcode:2011NatPh...7..725L. doi:10.1038/nphys2041. ISSN 1745-2473. S2CID 8992693.
- ^ Dean, M. P. M.; Springell, R. S.; Monney, C.; Zhou, K. J.; Pereiro, J.; et al. (2012-09-02). "Spin excitations in a single La2CuO4 layer". Nature Materials. 11 (10): 850–854. arXiv:1208.0018. Bibcode:2012NatMa..11..850D. doi:10.1038/nmat3409. ISSN 1476-1122. PMID 22941330. S2CID 6600719.
- ^ Dean, M. P. M.; Dellea, G.; Springell, R. S.; Yakhou-Harris, F.; Kummer, K.; et al. (2013-08-04). "Persistence of magnetic excitations in La2−xSrxCuO4 from the undoped insulator to the heavily overdoped non-superconducting metal". Nature Materials. 12 (11): 1019–1023. arXiv:1303.5359. Bibcode:2013NatMa..12.1019D. doi:10.1038/nmat3723. ISSN 1476-1122. PMID 23913170. S2CID 10231086.
- ^ Hancock, J. N.; Viennois, R.; van der Marel, D.; Rønnow, H. M.; Guarise, M.; et al. (2010-07-23). "Evidence for core-hole-mediated inelastic x-ray scattering from metallic Fe1.087Te". Physical Review B. 82 (2). American Physical Society (APS): 020513(R). arXiv:1004.3759. Bibcode:2010PhRvB..82b0513H. doi:10.1103/physrevb.82.020513. ISSN 1098-0121. S2CID 119225498.
- ^ Magnuson, M.; Schmitt, T.; Strocov, V. N.; Schlappa, J.; Kalabukhov, A. S.; Duda, L.-C. (2014-11-12). "Self-doping processes between planes and chains in the metal-to-superconductor transition of YBa2Cu3O6.9". Scientific Reports. 4 (1): 7017. arXiv:1411.3301. Bibcode:2014NatSR...4E7017M. doi:10.1038/srep07017. ISSN 2045-2322. PMC 4228345. PMID 25388860.
- ^ Guarise, M.; Piazza, B. Dalla; Berger, H.; Giannini, E.; Schmitt, T.; et al. (2014). "Anisotropic softening of magnetic excitations along the nodal direction in superconducting cuprates". Nature Communications. 5 (1). Springer Science and Business Media LLC: 5760. Bibcode:2014NatCo...5.5760G. doi:10.1038/ncomms6760. ISSN 2041-1723. PMID 25519803.
- ^ Guarise, M.; Dalla Piazza, B.; Moretti Sala, M.; Ghiringhelli, G.; Braicovich, L.; et al. (2010-10-08). "Measurement of Magnetic Excitations in the Two-Dimensional Antiferromagnetic Sr2CuO2Cl2 Insulator Using Resonant X-Ray Scattering: Evidence for Extended Interactions". Physical Review Letters. 105 (15): 157006. arXiv:1004.2441. Bibcode:2010PhRvL.105o7006G. doi:10.1103/physrevlett.105.157006. ISSN 0031-9007. PMID 21230933. S2CID 22995067.
- ^ Zhou, Ke-Jin; Huang, Yao-Bo; Monney, Claude; Dai, Xi; Strocov, Vladimir N.; et al. (2013-02-12). "Persistent high-energy spin excitations in iron-pnictide superconductors". Nature Communications. 4 (1). Springer Science and Business Media LLC: 1470. arXiv:1301.1289. Bibcode:2013NatCo...4.1470Z. doi:10.1038/ncomms2428. ISSN 2041-1723. PMID 23403571.
- ^ Kim, Young-June; Hill, J. P.; Yamaguchi, H.; Gog, T.; Casa, D. (2010-05-04). "Resonant inelastic x-ray scattering study of the electronic structure of Cu2O". Physical Review B. 81 (19): 195202. arXiv:0904.3937. Bibcode:2010PhRvB..81s5202K. doi:10.1103/physrevb.81.195202. ISSN 1098-0121. S2CID 117289462.
- ^ Grenier, S.; Hill, J. P.; Kiryukhin, V.; Ku, W.; Kim, Y.-J.; et al. (2005-02-03). "d−d Excitations in Manganites Probed by Resonant Inelastic X-Ray Scattering". Physical Review Letters. 94 (4). American Physical Society (APS): 047203. arXiv:cond-mat/0407326. Bibcode:2005PhRvL..94d7203G. doi:10.1103/physrevlett.94.047203. ISSN 0031-9007. PMID 15783591. S2CID 2908407.
- ^ Harada, Yoshihisa; Taguchi, Munetaka; Miyajima, Yoshiharu; Tokushima, Takashi; Horikawa, Yuka; et al. (2009-04-15). "Ligand Energy Controls the Heme-Fe Valence in Aqueous Myoglobins". Journal of the Physical Society of Japan. 78 (4). Physical Society of Japan: 044802. Bibcode:2009JPSJ...78d4802H. doi:10.1143/jpsj.78.044802. ISSN 0031-9015.
- ^ Glatzel, Pieter; Singh, Jagdeep; Kvashnina, Kristina O.; van Bokhoven, Jeroen A. (2010-03-03). "In Situ Characterization of the 5d Density of States of Pt Nanoparticles upon Adsorption of CO". Journal of the American Chemical Society. 132 (8). American Chemical Society (ACS): 2555–2557. doi:10.1021/ja907760p. ISSN 0002-7863. PMID 20121279.
- ^ Fuchs, O.; Zharnikov, M.; Weinhardt, L.; Blum, M.; Weigand, M.; et al. (2008-01-16). "Isotope and Temperature Effects in Liquid Water Probed by X-Ray Absorption and Resonant X-Ray Emission Spectroscopy". Physical Review Letters. 100 (2). American Physical Society (APS): 027801. Bibcode:2008PhRvL.100b7801F. doi:10.1103/physrevlett.100.027801. ISSN 0031-9007. PMID 18232928.
- ^ Tokushima, T.; Harada, Y.; Takahashi, O.; Senba, Y.; Ohashi, H.; Pettersson, L.G.M.; Nilsson, A.; Shin, S. (2008). "High resolution X-ray emission spectroscopy of liquid water: The observation of two structural motifs". Chemical Physics Letters. 460 (4–6). Elsevier BV: 387–400. Bibcode:2008CPL...460..387T. doi:10.1016/j.cplett.2008.04.077. ISSN 0009-2614.
- ^ Forsberg, Johan; Gråsjö, Johan; Brena, Barbara; Nordgren, Joseph; Duda, Laurent-C.; Rubensson, Jan-Erik (2009-04-13). "Angular anisotropy of resonant inelastic soft x-ray scattering from liquid water". Physical Review B. 79 (13). American Physical Society (APS): 132203. Bibcode:2009PhRvB..79m2203F. doi:10.1103/physrevb.79.132203. ISSN 1098-0121.
- ^ Yin, Zhong; Rajkovic, Ivan; Kubicek, Katharina; Quevedo, Wilson; Pietzsch, Annette; et al. (2014-07-28). "Probing the Hofmeister Effect with Ultrafast Core–Hole Spectroscopy". The Journal of Physical Chemistry B. 118 (31). American Chemical Society (ACS): 9398–9403. doi:10.1021/jp504577a. hdl:11858/00-001M-0000-0023-C074-7. ISSN 1520-6106. PMID 25029209.
- ^ Yin, Zhong; Rajkovic, Ivan; Thekku Veedu, Sreevidya; Deinert, Sascha; Raiser, Dirk; et al. (2015-01-28). "Ionic Solutions Probed by Resonant Inelastic X-ray Scattering". Zeitschrift für Physikalische Chemie. 229 (10–12). Walter de Gruyter GmbH: 1855. doi:10.1515/zpch-2015-0610. hdl:11858/00-001M-0000-0028-2D54-A. ISSN 0942-9352. S2CID 42044741.
- ^ Horikawa, Yuka; Tokushima, Takashi; Harada, Yoshihisa; Takahashi, Osamu; Chainani, Ashish; et al. (2009). "Identification of valence electronic states of aqueous acetic acid in acid–base equilibrium using site-selective X-ray emission spectroscopy". Physical Chemistry Chemical Physics. 11 (39). Royal Society of Chemistry (RSC): 8676–8679. Bibcode:2009PCCP...11.8676H. doi:10.1039/b910039c. ISSN 1463-9076. PMID 20449008.
- ^ Gråsjö, Johan; Andersson, Egil; Forsberg, Johan; Duda, Laurent; Henke, Ev; et al. (2009-12-10). "Local Electronic Structure of Functional Groups in Glycine As Anion, Zwitterion, and Cation in Aqueous Solution". The Journal of Physical Chemistry B. 113 (49). American Chemical Society (ACS): 16002–16006. doi:10.1021/jp905998x. ISSN 1520-6106. PMID 19916538.
- ^ Rueff, Jean-Pascal; Shukla, Abhay (2010-03-18). "Inelastic x-ray scattering by electronic excitations under high pressure". Reviews of Modern Physics. 82 (1): 847–896. arXiv:0812.0538. Bibcode:2010RvMP...82..847R. doi:10.1103/revmodphys.82.847. ISSN 0034-6861. S2CID 118507544.
- ^ Rossi, Matteo; Henriquet, Christian; Jacobs, Jeroen; Donnerer, Christian; Boseggia, Stefano; Al-Zein, Ali; Fumagalli, Roberto; Yao, Yi; Vale, James G.; Hunter, Emily C.; Perry, Robin S.; Kantor, Innokenty; Garbarino, Gaston; Crichton, Wilson; Monaco, Giulio (2019-08-15). "Resonant inelastic X-ray scattering of magnetic excitations under pressure". Journal of Synchrotron Radiation. 26 (5): 1725–1732. arXiv:1907.09519. doi:10.1107/s1600577519008877. ISSN 1600-5775.
Further reading
edit- Ament, Luuk JP, et al. "Resonant inelastic x-ray scattering studies of elementary excitations." Reviews of Modern Physics 83.2 (2011): 705.
- De Groot, Frank, and Akio Kotani. "Core level spectroscopy of solids" CRC press, 2008.
- Schülke, Winfried. "Electron dynamics by inelastic X-ray scattering" Vol. 7. OUP Oxford, 2007.
- Willmott, Philip. "An introduction to synchrotron radiation: techniques and applications" John Wiley & Sons, 2019.
External links
edit- Soft X-ray RIXS experiments at ESRF (European Synchrotron Radiation Facility).
- Hard X-ray RIXS experiments at ESRF (European Synchrotron Radiation Facility).
- RIXS experiments at SLS (Swiss Light Source).
- RIXS experiments at APS (Advanced Photon Source).
- RIXS experiments at SOLEIL (France).
- Soft X-ray RIXS experiment at SOLEIL (France).
- RIXS experiments at DLS (Diamond Light Source)



