In the mathematical discipline of graph theory, the (m,n)-lollipop graph is a special type of graph consisting of a complete graph (clique) on m vertices and a path graph on n vertices, connected with a bridge. [1]
| Lollipop graph | |
|---|---|
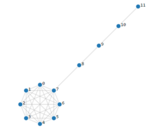 A (8,4)-lollipop graph | |
| Vertices | |
| Edges | |
| Girth | |
| Properties | connected |
| Notation | |
| Table of graphs and parameters | |
The special case of the (2n/3,n/3)-lollipop graphs are known as graphs which achieve the maximum possible hitting time,[2] cover time[3] and commute time.[4]
See also
edit- Barbell graph
- Tadpole graph
References
edit- ^ Weisstein, Eric. "Lollipop Graph". Wolfram Mathworld. Wolfram MathWorld. Retrieved 19 August 2015.
- ^ Brightwell, Graham; Winkler, Peter (September 1990). "Maximum hitting time for random walks on graphs". Random Structures & Algorithms. 1 (3): 263–276. doi:10.1002/rsa.3240010303.
- ^ Feige, Uriel (August 1995). "A tight upper bound on the cover time for random walks on graphs". Random Structures & Algorithms. 6: 51–54. CiteSeerX 10.1.1.38.1188. doi:10.1002/rsa.3240060106.
- ^ Jonasson, Johan (March 2000). "Lollipop graphs are extremal for commute times". Random Structures and Algorithms. 16 (2): 131–142. doi:10.1002/(SICI)1098-2418(200003)16:2<131::AID-RSA1>3.0.CO;2-3.
 | This graph theory-related article is a stub. You can help Wikipedia by expanding it. |