Limiting parallel

In neutral or absolute geometry, and in hyperbolic geometry, there may be many lines parallel to a given line $l$ through a point $P$ not on line $R$ ; however, in the plane, two parallels may be closer to $l$ than all others (one in each direction of $R$ ).

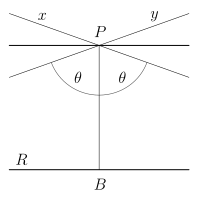
Thus it is useful to make a new definition concerning parallels in neutral geometry. If there are closest parallels to a given line they are known as the limiting parallel, asymptotic parallel or horoparallel (horo from Greek: ὅριον — border).

For rays, the relation of limiting parallel is an equivalence relation, which includes the equivalence relation of being coterminal.

If, in a hyperbolic triangle, the pairs of sides are limiting parallel, then the triangle is an ideal triangle.

Definition

The ray Aa is a limiting parallel to Bb, written:

Aa|||Bb

A ray $Aa$ is a limiting parallel to a ray $Bb$ if they are coterminal or if they lie on distinct lines not equal to the line $AB$ , they do not meet, and every ray in the interior of the angle $BAa$ meets the ray $Bb$ .^[1]

Properties

Distinct lines carrying limiting parallel rays do not meet.

Proof

Suppose that the lines carrying distinct parallel rays met. By definition they cannot meet on the side of $AB$ which either $a$ is on. Then they must meet on the side of $AB$ opposite to $a$ , call this point $C$ . Thus $\angle CAB+\angle CBA<2{\text{ right angles}}\Rightarrow \angle aAB+\angle bBA>2{\text{ right angles}}$ . Contradiction.

References

^ Hartshorne, Robin (2000). Geometry: Euclid and beyond (Corr. 2nd print. ed.). New York, NY [u.a.]: Springer. ISBN 978-0-387-98650-0.

[1] Hartshorne, Robin (2000). Geometry: Euclid and beyond (Corr. 2nd print. ed.). New York, NY [u.a.]: Springer. ISBN 978-0-387-98650-0.

[1]

Limiting parallel

Contents

Definition

Properties

Proof

See also

References