Gravitational memory effects, also known as gravitational-wave memory effects are predicted persistent changes in the relative position of pairs of masses in space due to the passing of a gravitational wave.[2] Detection of gravitational memory effects has been suggested as a way of validating general relativity.[3][4]
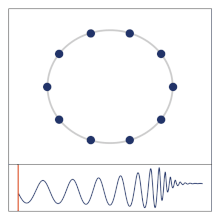
In 2014 Andrew Strominger and Alexander Zhiboedov showed that the formula related to the memory effect is the Fourier transform in time of Weinberg's soft graviton theorem.[5]
Linear and non linear effect
editThere are two kinds of predicted gravitational memory effect: one based on a linear approximation of Einstein's equations, first proposed in 1974 by the Soviet scientists Yakov Zel'dovich and A. G. Polnarev,[2][6] developed also by Vladimir Braginsky and L. P. Grishchuk,[2] and a non-linear phenomenon known as the non-linear memory effect, which was first proposed in the 1990s by Demetrios Christodoulou.[7][8][9]
The non-linear memory effect could be exploited to determine the inclination, with respect to us observers, of the plane on which the two objects that merged and generated the gravitational waves were moving, making the calculation of their distance more precise, since the amplitude of the received wave (what is experimentally measured) depends on the distance of the source and the aforementioned inclination with respect to us.[10]
Gravitational spin memory
editIn 2016, a new type of memory effect, induced by gravitational waves incident on rays of light moving along circular trajectories perpendicular to the waves, was proposed by Sabrina Gonzalez Pasterski, Strominger and Zhiboedov. This is caused by the angular momentum of the waves themselves and therefore termed gravitational spin memory. As in the previous case, this memory also turns out to be a Fourier transform in time, but, in this case, of the graviton theorem expanded to the subleading term.[11][12]
Detection
editThe effect should, in theory, be detectable by recording changes in the distance between pairs of free-falling objects in spacetime before and after the passage of gravitational waves. The proposed LISA detector is expected to detect the memory effect easily.[13] In contrast, detection with the existing LIGO is complicated by two factors. First, LIGO detection targets a higher frequency range than is desirable for detection of memory effects. Secondly, LIGO is not in free-fall, and its parts will drift back to their equilibrium position following the passage of the gravitational waves. However, as thousands of events from LIGO and similar earth-based detectors are recorded and statistically analyzed over the course of several years, the cumulative data may be sufficient to confirm the existence of the gravitational memory effect.[14]
See also
editReferences
edit- ^ Mitman, Keefe (2024-10-22). "A review of gravitational memory and BMS frame fixing in numerical relativity". Classical and Quantum Gravity. 41 (22). arXiv:2405.08868. doi:10.1088/1361-6382/ad83c2.
- ^ a b c Gibbons, G. W. (July 4, 2017). "The gravitational memory effect: what it is and why Stephen and I did not discover it" (PDF).
- ^ ARC Centre of Excellence for Gravitational Wave Discovery (February 4, 2020). "Astronomers search for gravitational-wave memory". phys.org. Retrieved 2020-07-31.
- ^ Zosso, Jann; Heisenberg, Lavinia; Yunes, Nicolás (2023). "Gravitational wave memory beyond general relativity". Phys. Rev. D. 108 (2): 024010. arXiv:2303.02021. doi:10.1103/PhysRevD.108.024010.
- ^ Strominger, Andrew; Zhiboedov, Alexander (2014). "Gravitational Memory, BMS Supertranslations and Soft Theorems". arXiv:1411.5745 [hep-th].
- ^ Ya. B. Zel’dovich and A. G. Polnarev, “Radiation of gravitational waves by a cluster of superdense stars,” Astron. Zh. 51, 30 (1974) [Sov. Astron. 18 17(1974)].
- ^ Christodoulou, Demetrios (1991-09-16). "Nonlinear nature of gravitation and gravitational-wave experiments". Physical Review Letters. 67 (12): 1486–1489. Bibcode:1991PhRvL..67.1486C. doi:10.1103/PhysRevLett.67.1486. ISSN 0031-9007. PMID 10044168.
- ^ Favata, Marc. "Gravitational-wave memory: an overview" (PDF).
- ^ Choi, Charles (12 October 2016). "Gravitational Waves May Permanently Alter Spacetime". www.pbs.org. WGBH/Nova. Retrieved 9 December 2021.
- ^ Xu, Yumeng; Rosselló-Sastre, Maria; Tiwari, Shubhanshu; Ebersold, Michael; Hamilton, Eleanor Z.; García-Quirós, Cecilio; Estellés, Héctor; Husa, Sascha (2024). "Enhancing gravitational wave parameter estimation with nonlinear memory: Breaking the distance-inclination degeneracy". Physical Review D. 109 (12): 123034. arXiv:2403.00441. doi:10.1103/PhysRevD.109.123034.
- ^ The formula for the soft graviton theorem is based on a Laurent series expansion. Weinberg calculations were limited to the first term of order -1.
- ^ Pasterski, Sabrina; Strominger, Andrew; Zhiboedov, Alexander (14 December 2016). "New gravitational memories". Journal of High Energy Physics. 2016 (12): 53. arXiv:1502.06120. Bibcode:2016JHEP...12..053P. doi:10.1007/JHEP12(2016)053. S2CID 256045385.
- ^ Inchauspé, Henri; Gasparotto, Silvia; Blas, Diego; Heisenberg, Lavinia; Zosso, Jann; Tiwari, Shubhanshu (2024). "Measuring gravitational wave memory with LISA". arXiv:2406.09228 [gr-qc].
- ^ McCormick, Katie (8 December 2021). "Gravitational Waves Should Permanently Distort Space-Time". Quanta Magazine. Retrieved 9 December 2021.
External links
edit- Gravitational-wave memory: an overview by Marc Favata
- The gravitational memory effect: what it is and why Stephen and I did not discover it by Gary Gibbons
- Sutter, Paul M. "Could Gravitational-Wave 'Memories' Prove Einstein Wrong?". Scientific American. Retrieved 2024-04-12.