Gazzi-Dickinson method

The Gazzi-Dickinson method is a point-counting technique used in geology to statistically measure the components of a sedimentary rock, chiefly sandstone. The main focus (and most controversial) part of the technique is counting all sand-sized components as separate grains, regardless of what they are connected to. Gazzi-Dickinson point counting is used in the creation of ternary diagrams, such as QFL diagrams.

A sand grain that could be used for the Gazzi-Dickinson method. Scale box in millimeters, plane-polarized light on top, cross-polarized light on bottom. Landing on the large phenocryst of amphibole (center, clear in plane light, orange in cross-polarized light) would count as a mineral grain in the Gazzi-Dickinson method because it is sand-sized. Landing on the plagioclase-rich groundmass surrounding the grain would count as a volcanic lithic fragment. It would count as a volcanic rock fragment in the Folk Classification/QFR classification regardless of where the microscope landed in the point count.

Technique

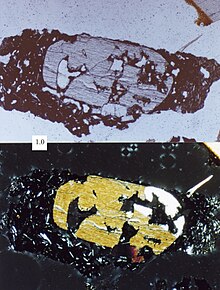
To perform a point count using the Gazzi-Dickinson method, a randomly selected thin section from a sedimentary rock is needed, with a slide advance mechanism that will randomly select points on the slide with a petrographic microscope. A minimum of 300 representative points (preferably 500 points) should be used to perform the count. On each randomly selected point that lands on a sand grain, the operator must determine the make-up of the area chosen, i.e. whether it is a mineral grain that is sand sized (larger than 62.5 micrometers) or a finer-grained fragment of another rock type, called a lithic fragment (e.g. a sand-sized piece of shale). These counts are then converted to percentages and used for compositional comparisons in provenance studies. Typically, only framework (non-matrix) grains are counted, or non-framework grains are counted and then excluded from percentages when using descriptive devices such as QFL triangles. This can create problems with pseudomatrix, which are lithic grains that have been deformed and thus blend in with (or have become) matrix.

History

The Gazzi-Dickinson method came out of separate work by P. Gazzi in 1966 and William R. Dickinson, starting in 1970. Dickinson and his students (most notably Raymond Ingersoll, Steven Graham, and Chris Suczek) at Stanford University in the 1970s established the method and its use to use the composition of sandstones to infer tectonic processes. This was in contrast to ideas presented by sedimentary geologists at Indiana University at the time, who used the more traditional "QFR" or "rock fragment" method of Robert Folk (1974) (which later grew into the Folk classification scheme), in which all grains that are connected are considered rock fragments, and the individual components are disregarded.

The best way to explain the differences in these two schools of thought is with an example: A sand rich in grus, or a granitic sand, when point counted with these two methods would yield drastically different results. A QFR-style count would be rich in rock fragments, whereas a Gazzi-Dickinson point count would show the sand rich in quartz and feldspar. Proponents of the Indiana University method would say that information is lost by not counting rock fragments. Proponents of Gazzi-Dickinson point counting would say that small changes in erosional transport would change the composition of the sand.

See also

• Folk classification