Conic constant

In geometry, the conic constant (or Schwarzschild constant, after Karl Schwarzschild) is a quantity describing conic sections, and is represented by the letter K. The constant is given by $$K=-e^{2},$$ where e is the eccentricity of the conic section.

An illustration of various conic constants

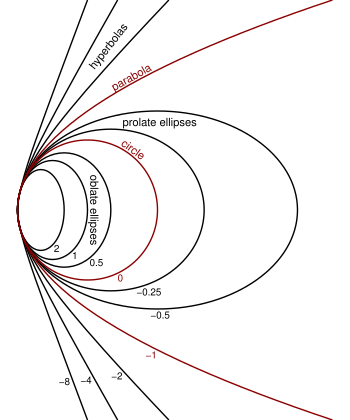
The equation for a conic section with apex at the origin and tangent to the y axis is $$y^{2}-2Rx+(K+1)x^{2}=0$$ alternately $$x={\dfrac {y^{2}}{R+{\sqrt {R^{2}-(K+1)y^{2}}}}}$$ where R is the radius of curvature at x = 0.

This formulation is used in geometric optics to specify oblate elliptical (K > 0), spherical (K = 0), prolate elliptical (0 > K > −1), parabolic (K = −1), and hyperbolic (K < −1) lens and mirror surfaces. When the paraxial approximation is valid, the optical surface can be treated as a spherical surface with the same radius.

References

• Smith, Warren J. (2008). Modern Optical Engineering, 4th ed. McGraw-Hill Professional. pp. 512–515. ISBN 978-0-07-147687-4.