Complex number

In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted i, called the imaginary unit and satisfying the equation $i^{2}=-1$; every complex number can be expressed in the form $a+bi$, where a and b are real numbers. Because no real number satisfies the above equation, i was called an imaginary number by René Descartes. For the complex number $a+bi$, a is called the real part, and b is called the imaginary part. The set of complex numbers is denoted by either of the symbols $\mathbb {C}$ or C. Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world.

A complex number can be visually represented as a pair of numbers (a, b) forming a vector on a diagram called an Argand diagram, representing the complex plane. Re is the real axis, Im is the imaginary axis, and i is the "imaginary unit", that satisfies i² = −1.

Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficients has a solution which is a complex number. For example, the equation $(x+1)^{2}=-9$ has no real solution, because the square of a real number cannot be negative, but has the two nonreal complex solutions $-1+3i$ and $-1-3i$.

Addition, subtraction and multiplication of complex numbers can be naturally defined by using the rule $i^{2}=-1$ along with the associative, commutative, and distributive laws. Every nonzero complex number has a multiplicative inverse. This makes the complex numbers a field with the real numbers as a subfield.

The complex numbers also form a real vector space of dimension two, with $\{1,i\}$ as a standard basis. This standard basis makes the complex numbers a Cartesian plane, called the complex plane. This allows a geometric interpretation of the complex numbers and their operations, and conversely some geometric objects and operations can be expressed in terms of complex numbers. For example, the real numbers form the real line, which is pictured as the horizontal axis of the complex plane, while real multiples of $i$ are the vertical axis. A complex number can also be defined by its geometric polar coordinates: the radius is called the absolute value of the complex number, while the angle from the positive real axis is called the argument of the complex number. The complex numbers of absolute value one form the unit circle. Adding a fixed complex number to all complex numbers defines a translation in the complex plane, and multiplying by a fixed complex number is a similarity centered at the origin (dilating by the absolute value, and rotating by the argument). The operation of complex conjugation is the reflection symmetry with respect to the real axis.

The complex numbers form a rich structure that is simultaneously an algebraically closed field, a commutative algebra over the reals, and a Euclidean vector space of dimension two.

Definition and basic operations

Various complex numbers depicted in the complex plane.

A complex number is an expression of the form a + bi, where a and b are real numbers, and i is an abstract symbol, the so-called imaginary unit, whose meaning will be explained further below. For example, 2 + 3i is a complex number.

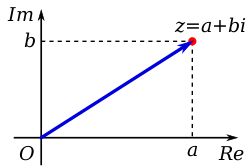
For a complex number a + bi, the real number a is called its real part , and the real number b (not the complex number bi) is its imaginary part. The real part of a complex number z is denoted Re(z), ${\mathcal {Re}}(z)$, or ${\mathfrak {R}}(z)$; the imaginary part is Im(z), ${\mathcal {Im}}(z)$, or ${\mathfrak {I}}(z)$: for example,${\textstyle \operatorname {Re} (2+3i)=2}$, $\operatorname {Im} (2+3i)=3$.

A complex number z can be identified with the ordered pair of real numbers $(\Re (z),\Im (z))$, which may be interpreted as coordinates of a point in a Euclidean plane with standard coordinates, which is then called the complex plane or Argand diagram,. The horizontal axis is generally used to display the real part, with increasing values to the right, and the imaginary part marks the vertical axis, with increasing values upwards.

A complex number z, as a point (black) and its position vector (blue).

A real number a can be regarded as a complex number a + 0i, whose imaginary part is 0. A purely imaginary number bi is a complex number 0 + bi, whose real part is zero. As with polynomials, it is common to write a + 0i = a, 0 + bi = bi, and a + (−b)i = a − bi; for example, 3 + (−4)i = 3 − 4i.

The set of all complex numbers is denoted by $\mathbb {C}$ (blackboard bold) or C (upright bold).

In some disciplines such as electromagnetism and electrical engineering, j is used instead of i, as i frequently represents electric current, and complex numbers are written as a + bj or a + jb.

Addition and subtraction

Addition of two complex numbers can be done geometrically by constructing a parallelogram.

Two complex numbers $a=x+yi$ and $b=u+vi$ are added by separately adding their real and imaginary parts. That is to say:

$$a+b=(x+yi)+(u+vi)=(x+u)+(y+v)i.$$ Similarly, subtraction can be performed as $$a-b=(x+yi)-(u+vi)=(x-u)+(y-v)i.$$

The addition can be geometrically visualized as follows: the sum of two complex numbers a and b, interpreted as points in the complex plane, is the point obtained by building a parallelogram from the three vertices O, and the points of the arrows labeled a and b (provided that they are not on a line). Equivalently, calling these points A, B, respectively and the fourth point of the parallelogram X the triangles OAB and XBA are congruent.

Multiplication

The product of two complex numbers is computed as follows:

$(a+bi)\cdot (c+di)=ac-bd+(ad+bc)i.$

For example, $(3+2i)(4-i)=3\cdot 4-(2\cdot (-1))+(3\cdot (-1)+2\cdot 4)i=14+5i.$ In particular, this includes as a special case the fundamental formula

$i^{2}=i\cdot i=-1.$

This formula distinguishes the complex number i from any real number, since the square of any (negative or positive) real number is always a non-negative real number.

With this definition of multiplication and addition, familiar rules for the arithmetic of rational or real numbers continue to hold for complex numbers. More precisely, the distributive property, the commutative properties (of addition and multiplication) hold. Therefore, the complex numbers form an algebraic structure known as a field, the same way as the rational or real numbers do.

Complex conjugate, absolute value, argument and division

Geometric representation of z and its conjugate z in the complex plane.

The complex conjugate of the complex number z = x + yi is defined as ${\overline {z}}=x-yi.$ It is also denoted by some authors by $z^{*}$. Geometrically, z is the "reflection" of z about the real axis. Conjugating twice gives the original complex number: ${\overline {\overline {z}}}=z.$ A complex number is real if and only if it equals its own conjugate. The unary operation of taking the complex conjugate of a complex number cannot be expressed by applying only their basic operations addition, subtraction, multiplication and division.

Argument φ and modulus r locate a point in the complex plane.

For any complex number z = x + yi , the product

$z\cdot {\overline {z}}=(x+iy)(x-iy)=x^{2}+y^{2}$

is a non-negative real number. This allows to define the absolute value (or modulus or magnitude) of z to be the square root $$|z|={\sqrt {x^{2}+y^{2}}}.$$ By Pythagoras' theorem, $|z|$ is the distance from the origin to the point representing the complex number z in the complex plane. In particular, the circle of radius one around the origin consists precisely of the numbers z such that $|z|=1$. If $z=x=x+0i$ is a real number, then $|z|=|x|$: its absolute value as a complex number and as a real number are equal.

Using the conjugate, the reciprocal of a nonzero complex number $z=x+yi$ can be computed to be

$${\frac {1}{z}}={\frac {\bar {z}}{z{\bar {z}}}}={\frac {\bar {z}}{|z|^{2}}}={\frac {x-yi}{x^{2}+y^{2}}}={\frac {x}{x^{2}+y^{2}}}-{\frac {y}{x^{2}+y^{2}}}i.$$ More generally, the division of an arbitrary complex number $w=u+vi$ by a non-zero complex number $z=x+yi$ equals $${\frac {w}{z}}={\frac {w{\bar {z}}}{|z|^{2}}}={\frac {(u+vi)(x-iy)}{x^{2}+y^{2}}}={\frac {ux+vy}{x^{2}+y^{2}}}+{\frac {vx-uy}{x^{2}+y^{2}}}i.$$ This process is sometimes called "rationalization" of the denominator (although the denominator in the final expression may be an irrational real number), because it resembles the method to remove roots from simple expressions in a denominator.

The argument of z (sometimes called the "phase" φ) is the angle of the radius Oz with the positive real axis, and is written as arg z, expressed in radians in this article. The angle is defined only up to adding integer multiples of $2\pi$, since a rotation by $2\pi$ (or 360°) around the origin leaves all points in the complex plane unchanged. One possible choice to uniquely specify the argument is to require it to be within the interval $(-\pi ,\pi ]$, which is referred to as the principal value. The argument can be computed from the rectangular form x + yi by means of the arctan (inverse tangent) function.

Polar form

Main article: Polar coordinate system

"Polar form" redirects here. For the higher-dimensional analogue, see Polar decomposition.

Multiplication of 2 + i (blue triangle) and 3 + i (red triangle). The red triangle is rotated to match the vertex of the blue one (the adding of both angles in the terms φ₁+φ₂ in the equation) and stretched by the length of the hypotenuse of the blue triangle (the multiplication of both radiuses, as per term r₁r₂ in the equation).

For any complex number z, with absolute value $r=|z|$ and argument $\varphi$, the equation

$z=r(\cos \varphi +i\sin \varphi )$

holds. This identity is referred to as the polar form of z. It is sometimes abbreviated as ${\textstyle z=r\operatorname {\mathrm {cis} } \varphi }$. In electronics, one represents a phasor with amplitude r and phase φ in angle notation:$$z=r\angle \varphi .$$

If two complex numbers are given in polar form, i.e., z₁ = r₁(cos φ₁ + i sin φ₁) and z₂ = r₂(cos φ₂ + i sin φ₂), the product and division can be computed as $$z_{1}z_{2}=r_{1}r_{2}(\cos(\varphi _{1}+\varphi _{2})+i\sin(\varphi _{1}+\varphi _{2})).$$ $${\frac {z_{1}}{z_{2}}}={\frac {r_{1}}{r_{2}}}\left(\cos(\varphi _{1}-\varphi _{2})+i\sin(\varphi _{1}-\varphi _{2})\right),{\text{if }}z_{2}\neq 0.$$ (These are a consequence of the trigonometric identities for the sine and cosine function.) In other words, the absolute values are multiplied and the arguments are added to yield the polar form of the product. The picture at the right illustrates the multiplication of $$(2+i)(3+i)=5+5i.$$ Because the real and imaginary part of 5 + 5i are equal, the argument of that number is 45 degrees, or π/4 (in radian). On the other hand, it is also the sum of the angles at the origin of the red and blue triangles are arctan(1/3) and arctan(1/2), respectively. Thus, the formula $${\frac {\pi }{4}}=\arctan \left({\frac {1}{2}}\right)+\arctan \left({\frac {1}{3}}\right)$$ holds. As the arctan function can be approximated highly efficiently, formulas like this – known as Machin-like formulas – are used for high-precision approximations of π: $${\frac {\pi }{4}}=4\arctan \left({\frac {1}{5}}\right)-\arctan \left({\frac {1}{239}}\right)$$

Powers and roots

See also: Square roots of negative and complex numbers

The n-th power of a complex number can be computed using de Moivre's formula, which is obtained by repeatedly applying the above formula for the product: $$z^{n}=\underbrace {z\cdot \dots \cdot z} _{n{\text{ factors}}}=(r(\cos \varphi +i\sin \varphi ))^{n}=r^{n}\,(\cos n\varphi +i\sin n\varphi ).$$ For example, the first few powers of the imaginary unit i are $i,i^{2}=-1,i^{3}=-i,i^{4}=1,i^{5}=i,\dots$.

Geometric representation of the 2nd to 6th roots of a complex number z, in polar form re^iφ  where r = |z | and φ = arg z. If z is real, φ = 0 or π. Principal roots are shown in black.

The n nth roots of a complex number z are given by $$z^{1/n}={\sqrt[{n}]{r}}\left(\cos \left({\frac {\varphi +2k\pi }{n}}\right)+i\sin \left({\frac {\varphi +2k\pi }{n}}\right)\right)$$ for 0 ≤ k ≤ n − 1. (Here ${\sqrt[{n}]{r}}$ is the usual (positive) nth root of the positive real number r.) Because sine and cosine are periodic, other integer values of k do not give other values. For any $z\neq 0$, there are, in particular n distinct complex n-th roots. For example, there are 4 fourth roots of 1, namely

$z_{1}=1,z_{2}=i,z_{3}=-1,z_{4}=-i.$

In general there is no natural way of distinguishing one particular complex nth root of a complex number. (This is in contrast to the roots of a positive real number x, which has a unique positive real n-th root, which is therefore commonly referred to as the n-th root of x.) One refers to this situation by saying that the nth root is a n-valued function of z.

Fundamental theorem of algebra

The fundamental theorem of algebra, of Carl Friedrich Gauss and Jean le Rond d'Alembert, states that for any complex numbers (called coefficients) a₀, ..., a_n, the equation $$a_{n}z^{n}+\dotsb +a_{1}z+a_{0}=0$$ has at least one complex solution z, provided that at least one of the higher coefficients a₁, ..., a_n is nonzero. This property does not hold for the field of rational numbers $\mathbb {Q}$ (the polynomial x² − 2 does not have a rational root, because √2 is not a rational number) nor the real numbers $\mathbb {R}$ (the polynomial x² + 4 does not have a real root, because the square of x is positive for any real number x).

Because of this fact, $\mathbb {C}$ is called an algebraically closed field. It is a cornerstone of various applications of complex numbers, as is detailed further below. There are various proofs of this theorem, by either analytic methods such as Liouville's theorem, or topological ones such as the winding number, or a proof combining Galois theory and the fact that any real polynomial of odd degree has at least one real root.

History

See also: Negative number § History

The solution in radicals (without trigonometric functions) of a general cubic equation, when all three of its roots are real numbers, contains the square roots of negative numbers, a situation that cannot be rectified by factoring aided by the rational root test, if the cubic is irreducible; this is the so-called casus irreducibilis ("irreducible case"). This conundrum led Italian mathematician Gerolamo Cardano to conceive of complex numbers in around 1545 in his Ars Magna, though his understanding was rudimentary; moreover, he later described complex numbers as being "as subtle as they are useless". Cardano did use imaginary numbers, but described using them as "mental torture." This was prior to the use of the graphical complex plane. Cardano and other Italian mathematicians, notably Scipione del Ferro, in the 1500s created an algorithm for solving cubic equations which generally had one real solution and two solutions containing an imaginary number. Because they ignored the answers with the imaginary numbers, Cardano found them useless.

Work on the problem of general polynomials ultimately led to the fundamental theorem of algebra, which shows that with complex numbers, a solution exists to every polynomial equation of degree one or higher. Complex numbers thus form an algebraically closed field, where any polynomial equation has a root.

Many mathematicians contributed to the development of complex numbers. The rules for addition, subtraction, multiplication, and root extraction of complex numbers were developed by the Italian mathematician Rafael Bombelli. A more abstract formalism for the complex numbers was further developed by the Irish mathematician William Rowan Hamilton, who extended this abstraction to the theory of quaternions.

The earliest fleeting reference to square roots of negative numbers can perhaps be said to occur in the work of the Greek mathematician Hero of Alexandria in the 1st century AD, where in his Stereometrica he considered, apparently in error, the volume of an impossible frustum of a pyramid to arrive at the term ${\sqrt {81-144}}$ in his calculations, which today would simplify to ${\sqrt {-63}}=3i{\sqrt {7}}$. Negative quantities were not conceived of in Hellenistic mathematics and Hero merely replaced it by its positive ${\sqrt {144-81}}=3{\sqrt {7}}.$

The impetus to study complex numbers as a topic in itself first arose in the 16th century when algebraic solutions for the roots of cubic and quartic polynomials were discovered by Italian mathematicians (Niccolò Fontana Tartaglia and Gerolamo Cardano). It was soon realized (but proved much later) that these formulas, even if one were interested only in real solutions, sometimes required the manipulation of square roots of negative numbers. In fact, it was proved later that the use of complex numbers is unavoidable when all three roots are real and distinct. However, the general formula can still be used in this case, with some care to deal with the ambiguity resulting from the existence of three cubic roots for nonzero complex numbers. Rafael Bombelli was the first to address explicitly these seemingly paradoxical solutions of cubic equations and developed the rules for complex arithmetic, trying to resolve these issues.

The term "imaginary" for these quantities was coined by René Descartes in 1637, who was at pains to stress their unreal nature:

... sometimes only imaginary, that is one can imagine as many as I said in each equation, but sometimes there exists no quantity that matches that which we imagine.
[... quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune quantité qui corresponde à celle qu'on imagine.]

A further source of confusion was that the equation ${\sqrt {-1}}^{2}={\sqrt {-1}}{\sqrt {-1}}=-1$ seemed to be capriciously inconsistent with the algebraic identity ${\sqrt {a}}{\sqrt {b}}={\sqrt {ab}}$, which is valid for non-negative real numbers a and b, and which was also used in complex number calculations with one of a, b positive and the other negative. The incorrect use of this identity in the case when both a and b are negative, and the related identity ${\textstyle {\frac {1}{\sqrt {a}}}={\sqrt {\frac {1}{a}}}}$, even bedeviled Leonhard Euler. This difficulty eventually led to the convention of using the special symbol i in place of ${\sqrt {-1}}$ to guard against this mistake. Even so, Euler considered it natural to introduce students to complex numbers much earlier than we do today. In his elementary algebra text book, Elements of Algebra, he introduces these numbers almost at once and then uses them in a natural way throughout.

In the 18th century complex numbers gained wider use, as it was noticed that formal manipulation of complex expressions could be used to simplify calculations involving trigonometric functions. For instance, in 1730 Abraham de Moivre noted that the identities relating trigonometric functions of an integer multiple of an angle to powers of trigonometric functions of that angle could be re-expressed by the following de Moivre's formula:

$$(\cos \theta +i\sin \theta )^{n}=\cos n\theta +i\sin n\theta .$$

Euler's formula relates the complex exponential function of an imaginary argument, which can be thought of as describing uniform circular motion in the complex plane, to the cosine and sine functions, geometrically its projections onto the real and imaginary axes, respectively.

In 1748, Euler went further and obtained Euler's formula of complex analysis:

$$e^{i\theta }=\cos \theta +i\sin \theta$$

by formally manipulating complex power series and observed that this formula could be used to reduce any trigonometric identity to much simpler exponential identities.

The idea of a complex number as a point in the complex plane (above) was first described by Danish–Norwegian mathematician Caspar Wessel in 1799, although it had been anticipated as early as 1685 in Wallis's A Treatise of Algebra.

Wessel's memoir appeared in the Proceedings of the Copenhagen Academy but went largely unnoticed. In 1806 Jean-Robert Argand independently issued a pamphlet on complex numbers and provided a rigorous proof of the fundamental theorem of algebra. Carl Friedrich Gauss had earlier published an essentially topological proof of the theorem in 1797 but expressed his doubts at the time about "the true metaphysics of the square root of −1". It was not until 1831 that he overcame these doubts and published his treatise on complex numbers as points in the plane, largely establishing modern notation and terminology:

If one formerly contemplated this subject from a false point of view and therefore found a mysterious darkness, this is in large part attributable to clumsy terminology. Had one not called +1, −1, ${\sqrt {-1}}$ positive, negative, or imaginary (or even impossible) units, but instead, say, direct, inverse, or lateral units, then there could scarcely have been talk of such darkness.

In the beginning of the 19th century, other mathematicians discovered independently the geometrical representation of the complex numbers: Buée, Mourey, Warren, Français and his brother, Bellavitis.

The English mathematician G.H. Hardy remarked that Gauss was the first mathematician to use complex numbers in "a really confident and scientific way" although mathematicians such as Norwegian Niels Henrik Abel and Carl Gustav Jacob Jacobi were necessarily using them routinely before Gauss published his 1831 treatise.

Augustin-Louis Cauchy and Bernhard Riemann together brought the fundamental ideas of complex analysis to a high state of completion, commencing around 1825 in Cauchy's case.

The common terms used in the theory are chiefly due to the founders. Argand called cos φ + i sin φ the direction factor, and $r={\sqrt {a^{2}+b^{2}}}$ the modulus; Cauchy (1821) called cos φ + i sin φ the reduced form (l'expression réduite) and apparently introduced the term argument; Gauss used i for ${\sqrt {-1}}$, introduced the term complex number for a + bi, and called a² + b² the norm. The expression direction coefficient, often used for cos φ + i sin φ, is due to Hankel (1867), and absolute value, for modulus, is due to Weierstrass.

Later classical writers on the general theory include Richard Dedekind, Otto Hölder, Felix Klein, Henri Poincaré, Hermann Schwarz, Karl Weierstrass and many others. Important work (including a systematization) in complex multivariate calculus has been started at beginning of the 20th century. Important results have been achieved by Wilhelm Wirtinger in 1927.

Abstract algebraic aspects

While the above low-level definitions, including the addition and multiplication, accurately describes the complex numbers, there are other, equivalent approaches that reveal the abstract algebraic structure of the complex numbers more immediately.

Construction as a quotient field

One approach to $\mathbb {C}$ is via polynomials, i.e., expressions of the form $$p(X)=a_{n}X^{n}+\dotsb +a_{1}X+a_{0},$$ where the coefficients a₀, ..., a_n are real numbers. The set of all such polynomials is denoted by $\mathbb {R} [X]$. Since sums and products of polynomials are again polynomials, this set $\mathbb {R} [X]$ forms a commutative ring, called the polynomial ring (over the reals). To every such polynomial p, one may assign the complex number $p(i)=a_{n}i^{n}+\dotsb +a_{1}i+a_{0}$, i.e., the value obtained by setting $X=i$. This defines a function

$\mathbb {R} [X]\to \mathbb {C}$

This function is surjective since every complex number can be obtained in such a way: the evaluation of a linear polynomial $a+bX$ at $X=i$ is $a+bi$. However, the evaluation of polynomial $X^{2}+1$ at i is 0, since $i^{2}+1=0.$ This polynomial is irreducible, i.e., cannot be written as a product of two linear polynomials. Basic facts of abstract algebra then imply that the kernel of the above map is an ideal generated by this polynomial, and that the quotient by this ideal is a field, and that there is an isomorphism

$\mathbb {R} [X]/(X^{2}+1){\stackrel {\cong }{\to }}\mathbb {C}$

between the quotient ring and $\mathbb {C}$. Some authors take this as the definition of $\mathbb {C}$.

Accepting that $\mathbb {C}$ is algebraically closed, because it is an algebraic extension of $\mathbb {R}$ in this approach, $\mathbb {C}$ is therefore the algebraic closure of $\mathbb {R} .$

Matrix representation of complex numbers

Complex numbers a + bi can also be represented by 2 × 2 matrices that have the form $${\begin{pmatrix}a&-b\\b&\;\;a\end{pmatrix}}.$$ Here the entries a and b are real numbers. As the sum and product of two such matrices is again of this form, these matrices form a subring of the ring of 2 × 2 matrices.

A simple computation shows that the map $$a+ib\mapsto {\begin{pmatrix}a&-b\\b&\;\;a\end{pmatrix}}$$ is a ring isomorphism from the field of complex numbers to the ring of these matrices, proving that these matrices form a field. This isomorphism associates the square of the absolute value of a complex number with the determinant of the corresponding matrix, and the conjugate of a complex number with the transpose of the matrix.

The geometric description of the multiplication of complex numbers can also be expressed in terms of rotation matrices by using this correspondence between complex numbers and such matrices. The action of the matrix on a vector (x, y) corresponds to the multiplication of x + iy by a + ib. In particular, if the determinant is 1, there is a real number t such that the matrix has the form

$${\begin{pmatrix}\cos t&-\sin t\\\sin t&\;\;\cos t\end{pmatrix}}.$$ In this case, the action of the matrix on vectors and the multiplication by the complex number $\cos t+i\sin t$ are both the rotation of the angle t.

Complex analysis

Main article: Complex analysis

The study of functions of a complex variable is known as complex analysis and has enormous practical use in applied mathematics as well as in other branches of mathematics. Often, the most natural proofs for statements in real analysis or even number theory employ techniques from complex analysis (see prime number theorem for an example).

A domain coloring graph of the function ⁠(z² − 1)(z − 2 − i)²/z² + 2 + 2i⁠. Darker spots mark moduli near zero, brighter spots are farther away from the origin. The color encodes the argument. The function has zeros for ±1, (2 + i) and poles at $\pm {\sqrt {-2-2i}}.$

Unlike real functions, which are commonly represented as two-dimensional graphs, complex functions have four-dimensional graphs and may usefully be illustrated by color-coding a three-dimensional graph to suggest four dimensions, or by animating the complex function's dynamic transformation of the complex plane.

Convergence

Illustration of the behavior of the sequence $z^{n}$ for three different values of z (all having the same argument): for $|z|<1$ the sequence converges to 0 (inner spiral), while it diverges for $|z|>1$ (outer spiral).

The notions of convergent series and continuous functions in (real) analysis have natural analogs in complex analysis. A sequence of complex numbers is said to converge if and only if its real and imaginary parts do. This is equivalent to the (ε, δ)-definition of limits, where the absolute value of real numbers is replaced by the one of complex numbers. From a more abstract point of view, $\mathbb {C}$, endowed with the metric $$\operatorname {d} (z_{1},z_{2})=|z_{1}-z_{2}|$$ is a complete metric space, which notably includes the triangle inequality $$|z_{1}+z_{2}|\leq |z_{1}|+|z_{2}|$$ for any two complex numbers z₁ and z₂.

Complex exponential

Illustration of the complex exponential function mapping the complex plane, w = exp ⁡(z). The left plane shows a square mesh with mesh size 1, with the three complex numbers 0, 1, and i highlighted. The two rectangles (in magenta and green) are mapped to circular segments, while the lines parallel to the x-axis are mapped to rays emanating from, but not containing the origin. Lines parallel to the y-axis are mapped to circles.

Like in real analysis, this notion of convergence is used to construct a number of elementary functions: the exponential function exp z, also written e^z, is defined as the infinite series, which can be shown to converge for any z: $$\exp z:=1+z+{\frac {z^{2}}{2\cdot 1}}+{\frac {z^{3}}{3\cdot 2\cdot 1}}+\cdots =\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}.$$ For example, $\exp(1)$ is Euler's number $e\approx 2.718$. Euler's formula states: $$\exp(i\varphi )=\cos \varphi +i\sin \varphi$$ for any real number φ. This formula is a quick consequence of general basic facts about convergent power series and the definitions of the involved functions as power series. As a special case, this includes Euler's identity $$\exp(i\pi )=-1.$$

Complex logarithm

The exponential function maps complex numbers z differing by a multiple of $2\pi i$ to the same complex number w.

For any positive real number t, there is a unique real number x such that $\exp(x)=t$. This leads to the definition of the natural logarithm as the inverse $\ln \colon \mathbb {R} ^{+}\to \mathbb {R} ;x\mapsto \ln x$ of the exponential function. The situation is different for complex numbers, since

$\exp(z+2\pi i)=\exp z\exp(2\pi i)=\exp z$

by the functional equation and Euler's identity. For example, e^iπ = e^3iπ = −1 , so both iπ and 3iπ are possible values for the complex logarithm of −1.

In general, given any non-zero complex number w, any number z solving the equation

$\exp z=w$

is called a complex logarithm of w, denoted $\log w$. It can be shown that these numbers satisfy $$z=\log w=\ln |w|+i\arg w,$$ where $\arg$ is the argument defined above, and $\ln$ the (real) natural logarithm. As arg is a multivalued function, unique only up to a multiple of 2π, log is also multivalued. The principal value of log is often taken by restricting the imaginary part to the interval (−π, π]. This leads to the complex logarithm being a bijective function taking values in the strip $\mathbb {R} ^{+}+\;i\,\left(-\pi ,\pi \right]$ (that is denoted $S_{0}$ in the above illustration) $$\ln \colon \;\mathbb {C} ^{\times }\;\to \;\;\;\mathbb {R} ^{+}+\;i\,\left(-\pi ,\pi \right].$$

If $z\in \mathbb {C} \setminus \left(-\mathbb {R} _{\geq 0}\right)$ is not a non-positive real number (a positive or a non-real number), the resulting principal value of the complex logarithm is obtained with −π < φ < π. It is an analytic function outside the negative real numbers, but it cannot be prolongated to a function that is continuous at any negative real number $z\in -\mathbb {R} ^{+}$, where the principal value is ln z = ln(−z) + iπ.

Complex exponentiation z^ω is defined as $$z^{\omega }=\exp(\omega \ln z),$$ and is multi-valued, except when ω is an integer. For ω = 1 / n, for some natural number n, this recovers the non-uniqueness of nth roots mentioned above. If z > 0 is real (and ω an arbitrary complex number), one has a preferred choice of $\ln x$, the real logarithm, which can be used to define a preferred exponential function.

Complex numbers, unlike real numbers, do not in general satisfy the unmodified power and logarithm identities, particularly when naïvely treated as single-valued functions; see failure of power and logarithm identities. For example, they do not satisfy $$a^{bc}=\left(a^{b}\right)^{c}.$$ Both sides of the equation are multivalued by the definition of complex exponentiation given here, and the values on the left are a subset of those on the right.

Complex sine and cosine

The series defining the real trigonometric functions sine and cosine, as well as the hyperbolic functions sinh and cosh, also carry over to complex arguments without change. For the other trigonometric and hyperbolic functions, such as tangent, things are slightly more complicated, as the defining series do not converge for all complex values. Therefore, one must define them either in terms of sine, cosine and exponential, or, equivalently, by using the method of analytic continuation.

Holomorphic functions

Color wheel graph of the function sin(1/z) that is holomorphic except at z = 0, which is an essential singularity of this function. White parts inside refer to numbers having large absolute values.

A function $f:\mathbb {C}$ → $\mathbb {C}$ is called holomorphic or complex differentiable at a point $z_{0}$ if the limit

$\lim _{z\to z_{0}}{f(z)-f(z_{0}) \over z-z_{0}}$

exists (in which case it is denoted by $f'(z_{0})$). This mimics the definition for real differentiable functions, except that all quantities are complex numbers. Loosely speaking, the freedom of approaching $z_{0}$ in different directions imposes a much stronger condition than being (real) differentiable. For example, the function

$f(z)={\overline {z}}$

is differentiable as a function $\mathbb {R} ^{2}\to \mathbb {R} ^{2}$, but is not complex differentiable. A real differentiable function is complex differentiable if and only if it satisfies the Cauchy–Riemann equations, which are sometimes abbreviated as

${\frac {\partial f}{\partial {\overline {z}}}}=0.$

Complex analysis shows some features not apparent in real analysis. For example, the identity theorem asserts that two holomorphic functions f and g agree if they agree on an arbitrarily small open subset of $\mathbb {C}$. Meromorphic functions, functions that can locally be written as f(z)/(z − z₀)ⁿ with a holomorphic function f, still share some of the features of holomorphic functions. Other functions have essential singularities, such as sin(1/z) at z = 0.

Applications

Complex numbers have applications in many scientific areas, including signal processing, control theory, electromagnetism, fluid dynamics, quantum mechanics, cartography, and vibration analysis. Some of these applications are described below.

Complex conjugation is also employed in inversive geometry, a branch of geometry studying reflections more general than ones about a line. In the network analysis of electrical circuits, the complex conjugate is used in finding the equivalent impedance when the maximum power transfer theorem is looked for.

Geometry

Shapes

Three non-collinear points $u,v,w$ in the plane determine the shape of the triangle $\{u,v,w\}$. Locating the points in the complex plane, this shape of a triangle may be expressed by complex arithmetic as $$S(u,v,w)={\frac {u-w}{u-v}}.$$ The shape $S$ of a triangle will remain the same, when the complex plane is transformed by translation or dilation (by an affine transformation), corresponding to the intuitive notion of shape, and describing similarity. Thus each triangle $\{u,v,w\}$ is in a similarity class of triangles with the same shape.

Fractal geometry

The Mandelbrot set with the real and imaginary axes labeled.

The Mandelbrot set is a popular example of a fractal formed on the complex plane. It is defined by plotting every location $c$ where iterating the sequence $f_{c}(z)=z^{2}+c$ does not diverge when iterated infinitely. Similarly, Julia sets have the same rules, except where $c$ remains constant.

Triangles

Every triangle has a unique Steiner inellipse – an ellipse inside the triangle and tangent to the midpoints of the three sides of the triangle. The foci of a triangle's Steiner inellipse can be found as follows, according to Marden's theorem: Denote the triangle's vertices in the complex plane as a = x_A + y_Ai, b = x_B + y_Bi, and c = x_C + y_Ci. Write the cubic equation $(x-a)(x-b)(x-c)=0$, take its derivative, and equate the (quadratic) derivative to zero. Marden's theorem says that the solutions of this equation are the complex numbers denoting the locations of the two foci of the Steiner inellipse.

Algebraic number theory

Construction of a regular pentagon using straightedge and compass.

As mentioned above, any nonconstant polynomial equation (in complex coefficients) has a solution in $\mathbb {C}$. A fortiori, the same is true if the equation has rational coefficients. The roots of such equations are called algebraic numbers – they are a principal object of study in algebraic number theory. Compared to ${\overline {\mathbb {Q} }}$, the algebraic closure of $\mathbb {Q}$, which also contains all algebraic numbers, $\mathbb {C}$ has the advantage of being easily understandable in geometric terms. In this way, algebraic methods can be used to study geometric questions and vice versa. With algebraic methods, more specifically applying the machinery of field theory to the number field containing roots of unity, it can be shown that it is not possible to construct a regular nonagon using only compass and straightedge – a purely geometric problem.

Another example is the Gaussian integers; that is, numbers of the form x + iy, where x and y are integers, which can be used to classify sums of squares.

Analytic number theory

Main article: Analytic number theory

Analytic number theory studies numbers, often integers or rationals, by taking advantage of the fact that they can be regarded as complex numbers, in which analytic methods can be used. This is done by encoding number-theoretic information in complex-valued functions. For example, the Riemann zeta function ζ(s) is related to the distribution of prime numbers.

Improper integrals

In applied fields, complex numbers are often used to compute certain real-valued improper integrals, by means of complex-valued functions. Several methods exist to do this; see methods of contour integration.

Dynamic equations

In differential equations, it is common to first find all complex roots r of the characteristic equation of a linear differential equation or equation system and then attempt to solve the system in terms of base functions of the form f(t) = e^rt. Likewise, in difference equations, the complex roots r of the characteristic equation of the difference equation system are used, to attempt to solve the system in terms of base functions of the form f(t) = r^t.

Linear algebra

Since $\mathbb {C}$ is algebraically closed, any non-empty complex square matrix has at least one (complex) eigenvalue. By comparison, real matrices do not always have real eigenvalues, for example rotation matrices (for rotations of the plane for angles other than 0° or 180°) leave no direction fixed, and therefore do not have any real eigenvalue. The existence of (complex) eigenvalues, and the ensuing existence of eigendecomposition is a useful tool for computing matrix powers and matrix exponentials.

Complex numbers often generalize concepts originally conceived in the real numbers. For example, the conjugate transpose generalizes the transpose, hermitian matrices generalize symmetric matrices, and unitary matrices generalize orthogonal matrices.

In applied mathematics

Control theory

See also: Complex plane § Use in control theory

In control theory, systems are often transformed from the time domain to the complex frequency domain using the Laplace transform. The system's zeros and poles are then analyzed in the complex plane. The root locus, Nyquist plot, and Nichols plot techniques all make use of the complex plane.

In the root locus method, it is important whether zeros and poles are in the left or right half planes, that is, have real part greater than or less than zero. If a linear, time-invariant (LTI) system has poles that are

• in the right half plane, it will be unstable,
• all in the left half plane, it will be stable,
• on the imaginary axis, it will have marginal stability.

If a system has zeros in the right half plane, it is a nonminimum phase system.

Signal analysis

Complex numbers are used in signal analysis and other fields for a convenient description for periodically varying signals. For given real functions representing actual physical quantities, often in terms of sines and cosines, corresponding complex functions are considered of which the real parts are the original quantities. For a sine wave of a given frequency, the absolute value |z| of the corresponding z is the amplitude and the argument arg z is the phase.

If Fourier analysis is employed to write a given real-valued signal as a sum of periodic functions, these periodic functions are often written as complex-valued functions of the form

$$x(t)=\operatorname {Re} \{X(t)\}$$

and

$$X(t)=Ae^{i\omega t}=ae^{i\phi }e^{i\omega t}=ae^{i(\omega t+\phi )}$$

where ω represents the angular frequency and the complex number A encodes the phase and amplitude as explained above.

This use is also extended into digital signal processing and digital image processing, which use digital versions of Fourier analysis (and wavelet analysis) to transmit, compress, restore, and otherwise process digital audio signals, still images, and video signals.

Another example, relevant to the two side bands of amplitude modulation of AM radio, is:

$${\begin{aligned}\cos((\omega +\alpha )t)+\cos \left((\omega -\alpha )t\right)&=\operatorname {Re} \left(e^{i(\omega +\alpha )t}+e^{i(\omega -\alpha )t}\right)\\&=\operatorname {Re} \left(\left(e^{i\alpha t}+e^{-i\alpha t}\right)\cdot e^{i\omega t}\right)\\&=\operatorname {Re} \left(2\cos(\alpha t)\cdot e^{i\omega t}\right)\\&=2\cos(\alpha t)\cdot \operatorname {Re} \left(e^{i\omega t}\right)\\&=2\cos(\alpha t)\cdot \cos \left(\omega t\right).\end{aligned}}$$

In physics

Electromagnetism and electrical engineering

Main article: Alternating current

In electrical engineering, the Fourier transform is used to analyze varying voltages and currents. The treatment of resistors, capacitors, and inductors can then be unified by introducing imaginary, frequency-dependent resistances for the latter two and combining all three in a single complex number called the impedance. This approach is called phasor calculus.

In electrical engineering, the imaginary unit is denoted by j, to avoid confusion with I, which is generally in use to denote electric current, or, more particularly, i, which is generally in use to denote instantaneous electric current.

Because the voltage in an AC circuit is oscillating, it can be represented as

$$V(t)=V_{0}e^{j\omega t}=V_{0}\left(\cos \omega t+j\sin \omega t\right),$$

To obtain the measurable quantity, the real part is taken:

$$v(t)=\operatorname {Re} (V)=\operatorname {Re} \left[V_{0}e^{j\omega t}\right]=V_{0}\cos \omega t.$$

The complex-valued signal V(t) is called the analytic representation of the real-valued, measurable signal v(t).

Fluid dynamics

In fluid dynamics, complex functions are used to describe potential flow in two dimensions.

Quantum mechanics

The complex number field is intrinsic to the mathematical formulations of quantum mechanics, where complex Hilbert spaces provide the context for one such formulation that is convenient and perhaps most standard. The original foundation formulas of quantum mechanics – the Schrödinger equation and Heisenberg's matrix mechanics – make use of complex numbers.

Relativity

In special and general relativity, some formulas for the metric on spacetime become simpler if one takes the time component of the spacetime continuum to be imaginary. (This approach is no longer standard in classical relativity, but is used in an essential way in quantum field theory.) Complex numbers are essential to spinors, which are a generalization of the tensors used in relativity.

Characterizations, generalizations and related notions

Algebraic characterization

The field $\mathbb {C}$ has the following three properties:

• First, it has characteristic 0. This means that 1 + 1 + ⋯ + 1 ≠ 0 for any number of summands (all of which equal one).
• Second, its transcendence degree over $\mathbb {Q}$, the prime field of $\mathbb {C} ,$ is the cardinality of the continuum.
• Third, it is algebraically closed (see above).

It can be shown that any field having these properties is isomorphic (as a field) to $\mathbb {C} .$ For example, the algebraic closure of the field $\mathbb {Q} _{p}$ of the p-adic number also satisfies these three properties, so these two fields are isomorphic (as fields, but not as topological fields). Also, $\mathbb {C}$ is isomorphic to the field of complex Puiseux series. However, specifying an isomorphism requires the axiom of choice. Another consequence of this algebraic characterization is that $\mathbb {C}$ contains many proper subfields that are isomorphic to $\mathbb {C}$.

Characterization as a topological field

The preceding characterization of $\mathbb {C}$ describes only the algebraic aspects of $\mathbb {C} .$ That is to say, the properties of nearness and continuity, which matter in areas such as analysis and topology, are not dealt with. The following description of $\mathbb {C}$ as a topological field (that is, a field that is equipped with a topology, which allows the notion of convergence) does take into account the topological properties. $\mathbb {C}$ contains a subset P (namely the set of positive real numbers) of nonzero elements satisfying the following three conditions:

• P is closed under addition, multiplication and taking inverses.
• If x and y are distinct elements of P, then either x − y or y − x is in P.
• If S is any nonempty subset of P, then S + P = x + P for some x in $\mathbb {C} .$

Moreover, $\mathbb {C}$ has a nontrivial involutive automorphism x ↦ x* (namely the complex conjugation), such that x x* is in P for any nonzero x in $\mathbb {C} .$

Any field F with these properties can be endowed with a topology by taking the sets B(x, p) = { y | p − (y − x)(y − x)* ∈ P }  as a base, where x ranges over the field and p ranges over P. With this topology F is isomorphic as a topological field to $\mathbb {C} .$

The only connected locally compact topological fields are $\mathbb {R}$ and $\mathbb {C} .$ This gives another characterization of $\mathbb {C}$ as a topological field, because $\mathbb {C}$ can be distinguished from $\mathbb {R}$ because the nonzero complex numbers are connected, while the nonzero real numbers are not.

Other number systems

Main articles: Cayley–Dickson construction, Quaternion, and Octonion

Number systems

	rational numbers $\mathbb {Q}$	real numbers $\mathbb {R}$	complex numbers $\mathbb {C}$	quaternions $\mathbb {H}$	octonions $\mathbb {O}$	sedenions $\mathbb {S}$
complete	No	Yes	Yes	Yes	Yes	Yes
dimension as an $\mathbb {R}$-vector space	[does not apply]	1	2	4	8	16
ordered	Yes	Yes	No	No	No	No
multiplication commutative ($xy=yx$)	Yes	Yes	Yes	No	No	No
multiplication associative ($(xy)z=x(yz)$)	Yes	Yes	Yes	Yes	No	No
normed division algebra (over $\mathbb {R}$)	[does not apply]	Yes	Yes	Yes	Yes	No

The process of extending the field $\mathbb {R}$ of reals to $\mathbb {C}$ is an instance of the Cayley–Dickson construction. Applying this construction iteratively to $\mathbb {C}$ then yields the quaternions, the octonions, the sedenions, and the trigintaduonions. This construction turns out to diminish the structural properties of the involved number systems.

Unlike the reals, $\mathbb {C}$ is not an ordered field, that is to say, it is not possible to define a relation z₁ < z₂ that is compatible with the addition and multiplication. In fact, in any ordered field, the square of any element is necessarily positive, so i² = −1 precludes the existence of an ordering on $\mathbb {C} .$ Passing from $\mathbb {C}$ to the quaternions $\mathbb {H}$ loses commutativity, while the octonions (additionally to not being commutative) fail to be associative. The reals, complex numbers, quaternions and octonions are all normed division algebras over $\mathbb {R}$. By Hurwitz's theorem they are the only ones; the sedenions, the next step in the Cayley–Dickson construction, fail to have this structure.

The Cayley–Dickson construction is closely related to the regular representation of $\mathbb {C} ,$ thought of as an $\mathbb {R}$-algebra (an $\mathbb {R}$-vector space with a multiplication), with respect to the basis (1, i). This means the following: the $\mathbb {R}$-linear map $${\begin{aligned}\mathbb {C} &\rightarrow \mathbb {C} \\z&\mapsto wz\end{aligned}}$$ for some fixed complex number w can be represented by a 2 × 2 matrix (once a basis has been chosen). With respect to the basis (1, i), this matrix is $${\begin{pmatrix}\operatorname {Re} (w)&-\operatorname {Im} (w)\\\operatorname {Im} (w)&\operatorname {Re} (w)\end{pmatrix}},$$ that is, the one mentioned in the section on matrix representation of complex numbers above. While this is a linear representation of $\mathbb {C}$ in the 2 × 2 real matrices, it is not the only one. Any matrix $$J={\begin{pmatrix}p&q\\r&-p\end{pmatrix}},\quad p^{2}+qr+1=0$$ has the property that its square is the negative of the identity matrix: J² = −I. Then $$\{z=aI+bJ:a,b\in \mathbb {R} \}$$ is also isomorphic to the field $\mathbb {C} ,$ and gives an alternative complex structure on $\mathbb {R} ^{2}.$ This is generalized by the notion of a linear complex structure.

Hypercomplex numbers also generalize $\mathbb {R} ,$ $\mathbb {C} ,$ $\mathbb {H} ,$ and $\mathbb {O} .$ For example, this notion contains the split-complex numbers, which are elements of the ring $\mathbb {R} [x]/(x^{2}-1)$ (as opposed to $\mathbb {R} [x]/(x^{2}+1)$ for complex numbers). In this ring, the equation a² = 1 has four solutions.

The field $\mathbb {R}$ is the completion of $\mathbb {Q} ,$ the field of rational numbers, with respect to the usual absolute value metric. Other choices of metrics on $\mathbb {Q}$ lead to the fields $\mathbb {Q} _{p}$ of p-adic numbers (for any prime number p), which are thereby analogous to $\mathbb {R}$. There are no other nontrivial ways of completing $\mathbb {Q}$ than $\mathbb {R}$ and $\mathbb {Q} _{p},$ by Ostrowski's theorem. The algebraic closures ${\overline {\mathbb {Q} _{p}}}$ of $\mathbb {Q} _{p}$ still carry a norm, but (unlike $\mathbb {C}$) are not complete with respect to it. The completion $\mathbb {C} _{p}$ of ${\overline {\mathbb {Q} _{p}}}$ turns out to be algebraically closed. By analogy, the field is called p-adic complex numbers.

The fields $\mathbb {R} ,$ $\mathbb {Q} _{p},$ and their finite field extensions, including $\mathbb {C} ,$ are called local fields.

See also

• Analytic continuation
• Circular motion using complex numbers
• Complex-base system
• Complex coordinate space
• Complex geometry
• Geometry of numbers
• Dual-complex number
• Eisenstein integer
• Geometric algebra (which includes the complex plane as the 2-dimensional spinor subspace ${\mathcal {G}}_{2}^{+}$)
• Unit complex number

References

• Ahlfors, Lars (1979). Complex analysis (3rd ed.). McGraw-Hill. ISBN 978-0-07-000657-7.
• Andreescu, Titu; Andrica, Dorin (2014), Complex Numbers from A to ... Z (Second ed.), New York: Springer, doi:10.1007/978-0-8176-8415-0, ISBN 978-0-8176-8414-3
• Apostol, Tom (1981). Mathematical analysis. Addison-Wesley.
• Aufmann, Richard N.; Barker, Vernon C.; Nation, Richard D. (2007). College Algebra and Trigonometry (6 ed.). Cengage Learning. ISBN 978-0-618-82515-8.
• Conway, John B. (1986). Functions of One Complex Variable I. Springer. ISBN 978-0-387-90328-6.
• Derbyshire, John (2006). Unknown Quantity: A real and imaginary history of algebra. Joseph Henry Press. ISBN 978-0-309-09657-7.
• Joshi, Kapil D. (1989). Foundations of Discrete Mathematics. New York: John Wiley & Sons. ISBN 978-0-470-21152-6.
• Needham, Tristan (1997). Visual Complex Analysis. Clarendon Press. ISBN 978-0-19-853447-1.
• Pedoe, Dan (1988). Geometry: A comprehensive course. Dover. ISBN 978-0-486-65812-4.
• Penrose, Roger (2005). The Road to Reality: A complete guide to the laws of the universe. Alfred A. Knopf. ISBN 978-0-679-45443-4.
• Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. (2007). "Section 5.5 Complex Arithmetic". Numerical Recipes: The art of scientific computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. Archived from the original on 13 March 2020. Retrieved 9 August 2011.
• Solomentsev, E.D. (2001) [1994], "Complex number", Encyclopedia of Mathematics, EMS Press

Historical references

• Argand (1814). "Reflexions sur la nouvelle théorie des imaginaires, suives d'une application à la demonstration d'un theorème d'analise" [Reflections on the new theory of complex numbers, followed by an application to the proof of a theorem of analysis]. Annales de mathématiques pures et appliquées (in French). 5: 197–209.
• Bourbaki, Nicolas (1998). "Foundations of mathematics § logic: set theory". Elements of the history of mathematics. Springer.
• Burton, David M. (1995). The History of Mathematics (3rd ed.). New York: McGraw-Hill. ISBN 978-0-07-009465-9.
• Gauss, C. F. (1831). "Theoria residuorum biquadraticorum. Commentatio secunda" [Theory of biquadratic residues. Second memoir.]. Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores (in Latin). 7: 89–148.
• Katz, Victor J. (2004). A History of Mathematics, Brief Version. Addison-Wesley. ISBN 978-0-321-16193-2.
• Nahin, Paul J. (1998). An Imaginary Tale: The Story of $\scriptstyle {\sqrt {-1}}$. Princeton University Press. ISBN 978-0-691-02795-1. — A gentle introduction to the history of complex numbers and the beginnings of complex analysis.
• Ebbinghaus, H. D.; Hermes, H.; Hirzebruch, F.; Koecher, M.; Mainzer, K.; Neukirch, J.; Prestel, A.; Remmert, R. (1991). Numbers (hardcover ed.). Springer. ISBN 978-0-387-97497-2. — An advanced perspective on the historical development of the concept of number.