This article needs additional citations for verification. (May 2011) |
Binary classification is the task of classifying the elements of a set into one of two groups (each called class). Typical binary classification problems include:
- Medical testing to determine if a patient has a certain disease or not;
- Quality control in industry, deciding whether a specification has been met;
- In information retrieval, deciding whether a page should be in the result set of a search or not
- In administration, deciding whether someone should be issued with a driving licence or not
- In cognition, deciding whether an object is food or not food.
When measuring the accuracy of a binary classifier, the simplest way is to count the errors. But in the real world often one of the two classes is more important, so that the number of both of the different types of errors is of interest. For example, in medical testing, detecting a disease when it is not present (a false positive) is considered differently from not detecting a disease when it is present (a false negative).
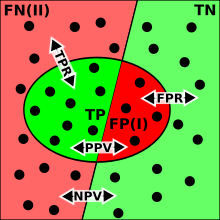
TP=true positive; TN=true negative; FP=false positive (type I error); FN=false negative (type II error); TPR=set of instances to determine true positive rate; FPR=set of instances to determine false positive rate; PPV=positive predictive value; NPV=negative predictive value.
Four outcomes
editGiven a classification of a specific data set, there are four basic combinations of actual data category and assigned category: true positives TP (correct positive assignments), true negatives TN (correct negative assignments), false positives FP (incorrect positive assignments), and false negatives FN (incorrect negative assignments).
Assigned Actual
|
Test outcome positive | Test outcome negative |
|---|---|---|
| Condition positive | True positive | False negative |
| Condition negative | False positive | True negative |
These can be arranged into a 2×2 contingency table, with rows corresponding to actual value – condition positive or condition negative – and columns corresponding to classification value – test outcome positive or test outcome negative.
Evaluation
editFrom tallies of the four basic outcomes, there are many approaches that can be used to measure the accuracy of a classifier or predictor. Different fields have different preferences.
The eight basic ratios
editA common approach to evaluation is to begin by computing two ratios of a standard pattern. There are eight basic ratios of this form that one can compute from the contingency table, which come in four complementary pairs (each pair summing to 1). These are obtained by dividing each of the four numbers by the sum of its row or column, yielding eight numbers, which can be referred to generically in the form "true positive row ratio" or "false negative column ratio".
There are thus two pairs of column ratios and two pairs of row ratios, and one can summarize these with four numbers by choosing one ratio from each pair – the other four numbers are the complements.
The row ratios are:
- true positive rate (TPR) = (TP/(TP+FN)), aka sensitivity or recall. These are the proportion of the population with the condition for which the test is correct.
- with complement the false negative rate (FNR) = (FN/(TP+FN))
- true negative rate (TNR) = (TN/(TN+FP), aka specificity (SPC),
- with complement false positive rate (FPR) = (FP/(TN+FP)), also called independent of prevalence
The column ratios are:
- positive predictive value (PPV, aka precision) (TP/(TP+FP)). These are the proportion of the population with a given test result for which the test is correct.
- with complement the false discovery rate (FDR) (FP/(TP+FP))
- negative predictive value (NPV) (TN/(TN+FN))
- with complement the false omission rate (FOR) (FN/(TN+FN)), also called dependence on prevalence.
In diagnostic testing, the main ratios used are the true column ratios – true positive rate and true negative rate – where they are known as sensitivity and specificity. In informational retrieval, the main ratios are the true positive ratios (row and column) – positive predictive value and true positive rate – where they are known as precision and recall.
Cullerne Bown has suggested a flow chart for determining which pair of indicators should be used when.[1] Otherwise, there is no general rule for deciding. There is also no general agreement on how the pair of indicators should be used to decide on concrete questions, such as when to prefer one classifier over another.
One can take ratios of a complementary pair of ratios, yielding four likelihood ratios (two column ratio of ratios, two row ratio of ratios). This is primarily done for the column (condition) ratios, yielding likelihood ratios in diagnostic testing. Taking the ratio of one of these groups of ratios yields a final ratio, the diagnostic odds ratio (DOR). This can also be defined directly as (TP×TN)/(FP×FN) = (TP/FN)/(FP/TN); this has a useful interpretation – as an odds ratio – and is prevalence-independent.
Other metrics
editThere are a number of other metrics, most simply the accuracy or Fraction Correct (FC), which measures the fraction of all instances that are correctly categorized; the complement is the Fraction Incorrect (FiC). The F-score combines precision and recall into one number via a choice of weighing, most simply equal weighing, as the balanced F-score (F1 score). Some metrics come from regression coefficients: the markedness and the informedness, and their geometric mean, the Matthews correlation coefficient. Other metrics include Youden's J statistic, the uncertainty coefficient, the phi coefficient, and Cohen's kappa.
Statistical binary classification
editStatistical classification is a problem studied in machine learning in which the classification is performed on the basis of a classification rule. It is a type of supervised learning, a method of machine learning where the categories are predefined, and is used to categorize new probabilistic observations into said categories. When there are only two categories the problem is known as statistical binary classification.
Some of the methods commonly used for binary classification are:
- Decision trees
- Random forests
- Bayesian networks
- Support vector machines
- Neural networks
- Logistic regression
- Probit model
- Genetic Programming
- Multi expression programming
- Linear genetic programming
Each classifier is best in only a select domain based upon the number of observations, the dimensionality of the feature vector, the noise in the data and many other factors. For example, random forests perform better than SVM classifiers for 3D point clouds.[2][3]
Converting continuous values to binary
editBinary classification may be a form of dichotomization in which a continuous function is transformed into a binary variable. Tests whose results are of continuous values, such as most blood values, can artificially be made binary by defining a cutoff value, with test results being designated as positive or negative depending on whether the resultant value is higher or lower than the cutoff.
However, such conversion causes a loss of information, as the resultant binary classification does not tell how much above or below the cutoff a value is. As a result, when converting a continuous value that is close to the cutoff to a binary one, the resultant positive or negative predictive value is generally higher than the predictive value given directly from the continuous value. In such cases, the designation of the test of being either positive or negative gives the appearance of an inappropriately high certainty, while the value is in fact in an interval of uncertainty. For example, with the urine concentration of hCG as a continuous value, a urine pregnancy test that measured 52 mIU/ml of hCG may show as "positive" with 50 mIU/ml as cutoff, but is in fact in an interval of uncertainty, which may be apparent only by knowing the original continuous value. On the other hand, a test result very far from the cutoff generally has a resultant positive or negative predictive value that is lower than the predictive value given from the continuous value. For example, a urine hCG value of 200,000 mIU/ml confers a very high probability of pregnancy, but conversion to binary values results in that it shows just as "positive" as the one of 52 mIU/ml.
See also
edit- Approximate membership query filter
- Examples of Bayesian inference
- Classification rule
- Confusion matrix
- Detection theory
- Kernel methods
- Multiclass classification
- Multi-label classification
- One-class classification
- Prosecutor's fallacy
- Receiver operating characteristic
- Thresholding (image processing)
- Uncertainty coefficient, aka proficiency
- Qualitative property
- Precision and recall (equivalent classification schema)
References
edit- ^ William Cullerne Bown (2024). "Sensitivity and Specificity versus Precision and Recall, and Related Dilemmas". Journal of Classification. 41 (2): 402–426. doi:10.1007/s00357-024-09478-y.
- ^ Zhang & Zakhor, Richard & Avideh (2014). "Automatic Identification of Window Regions on Indoor Point Clouds Using LiDAR and Cameras". VIP Lab Publications. CiteSeerX 10.1.1.649.303.
- ^ Y. Lu and C. Rasmussen (2012). "Simplified markov random fields for efficient semantic labeling of 3D point clouds" (PDF). IROS.
Bibliography
edit- Nello Cristianini and John Shawe-Taylor. An Introduction to Support Vector Machines and other kernel-based learning methods. Cambridge University Press, 2000. ISBN 0-521-78019-5 ([1] SVM Book)
- John Shawe-Taylor and Nello Cristianini. Kernel Methods for Pattern Analysis. Cambridge University Press, 2004. ISBN 0-521-81397-2 (Website for the book)
- Bernhard Schölkopf and A. J. Smola: Learning with Kernels. MIT Press, Cambridge, Massachusetts, 2002. ISBN 0-262-19475-9