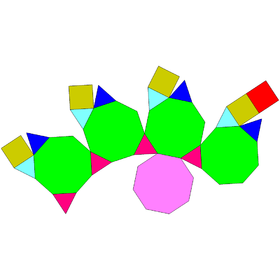
In geometry, the augmented truncated cube is one of the Johnson solids (J66). As its name suggests, it is created by attaching a square cupola (J4) onto one octagonal face of a truncated cube.
| Augmented truncated cube | |
|---|---|
 | |
| Type | Johnson J65 – J66 – J67 |
| Faces | 3x4 triangles 1+4 squares 1+4 octagons |
| Edges | 48 |
| Vertices | 28 |
| Vertex configuration | 2.4+8(3.82) 4(3.43) 8(3.4.3.8) |
| Symmetry group | C4v |
| Dual polyhedron | - |
| Properties | convex |
| Net | |
 | |
A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.[1]
References
edit- Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- Victor A. Zalgaller (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. The first proof that there are only 92 Johnson solids.
External links
edit
- ^ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.