The Ailles rectangle is a rectangle constructed from four right-angled triangles which is commonly used in geometry classes to find the values of trigonometric functions of 15° and 75°.[1] It is named after Douglas S. Ailles who was a high school teacher at Kipling Collegiate Institute in Toronto.[2][3]
Construction
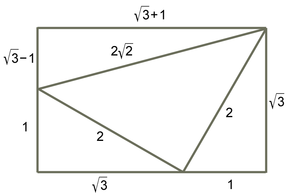
editA 30°–60°–90° triangle has sides of length 1, 2, and . When two such triangles are placed in the positions shown in the illustration, the smallest rectangle that can enclose them has width and height . Drawing a line connecting the original triangles' top corners creates a 45°–45°–90° triangle between the two, with sides of lengths 2, 2, and (by the Pythagorean theorem) . The remaining space at the top of the rectangle is a right triangle with acute angles of 15° and 75° and sides of , , and .
Derived trigonometric formulas
editFrom the construction of the rectangle, it follows that
and
Variant
editAn alternative construction (also by Ailles) places a 30°–60°–90° triangle in the middle with sidelengths of , , and . Its legs are each the hypotenuse of a 45°–45°–90° triangle, one with legs of length and one with legs of length .[4][5] The 15°–75°–90° triangle is the same as above.
See also
editReferences
edit- ^ Ravi Vakil (January 1996). A Mathematical Mosaic: Patterns & Problem Solving. Brendan Kelly Publishing Inc. pp. 87–. ISBN 978-1-895997-04-0.
ailles rectangle.
- ^ Charles P. McKeague; Mark D. Turner (1 January 2016). Trigonometry. Cengage Learning. pp. 124–. ISBN 978-1-305-65222-4.
- ^ DOUGLAS S. AILLES (1 October 1971). "Triangles and Trigonometry". The Mathematics Teacher. 64 (6): 562. doi:10.5951/MT.64.6.0562. JSTOR 27958618. Retrieved 2021-07-22.
- ^ "Third Ailles Rectangle". Stack Exchange. 11 February 2016. Retrieved 2017-11-01.
- ^ Colin Beveridge (31 August 2015). "The Mathematical Ninja and Ailles' Rectangle". Flying Colours Maths. Retrieved 2017-11-01.