In optical physics, transmittance of the surface of a material is its effectiveness in transmitting radiant energy. It is the fraction of incident electromagnetic power that is transmitted through a sample, in contrast to the transmission coefficient, which is the ratio of the transmitted to incident electric field.[2]
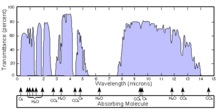

Internal transmittance refers to energy loss by absorption, whereas (total) transmittance is that due to absorption, scattering, reflection, etc.
Mathematical definitions
editHemispherical transmittance
editHemispherical transmittance of a surface, denoted T, is defined as[3]
where
- Φet is the radiant flux transmitted by that surface;
- Φei is the radiant flux received by that surface.
Spectral hemispherical transmittance
editSpectral hemispherical transmittance in frequency and spectral hemispherical transmittance in wavelength of a surface, denoted Tν and Tλ respectively, are defined as[3]
where
- Φe,νt is the spectral radiant flux in frequency transmitted by that surface;
- Φe,νi is the spectral radiant flux in frequency received by that surface;
- Φe,λt is the spectral radiant flux in wavelength transmitted by that surface;
- Φe,λi is the spectral radiant flux in wavelength received by that surface.
Directional transmittance
editDirectional transmittance of a surface, denoted TΩ, is defined as[3]
where
- Le,Ωt is the radiance transmitted by that surface;
- Le,Ωi is the radiance received by that surface.
Spectral directional transmittance
editSpectral directional transmittance in frequency and spectral directional transmittance in wavelength of a surface, denoted Tν,Ω and Tλ,Ω respectively, are defined as[3]
where
- Le,Ω,νt is the spectral radiance in frequency transmitted by that surface;
- Le,Ω,νi is the spectral radiance received by that surface;
- Le,Ω,λt is the spectral radiance in wavelength transmitted by that surface;
- Le,Ω,λi is the spectral radiance in wavelength received by that surface.
Luminous transmittance
editIn the field of photometry (optics), the luminous transmittance of a filter is a measure of the amount of luminous flux or intensity transmitted by an optical filter. It is generally defined in terms of a standard illuminant (e.g. Illuminant A, Iluminant C, or Illuminant E). The luminous transmittance with respect to the standard illuminant is defined as:
where:
- is the spectral radiant flux or intensity of the standard illuminant (unspecified magnitude).
- is the spectral transmittance of the filter
- is the luminous efficiency function
The luminous transmittance is independent of the magnitude of the flux or intensity of the standard illuminant used to measure it, and is a dimensionless quantity.
Beer–Lambert law
editBy definition, internal transmittance is related to optical depth and to absorbance as
where
- τ is the optical depth;
- A is the absorbance.
The Beer–Lambert law states that, for N attenuating species in the material sample,
or equivalently that
where
- σi is the attenuation cross section of the attenuating species i in the material sample;
- ni is the number density of the attenuating species i in the material sample;
- εi is the molar attenuation coefficient of the attenuating species i in the material sample;
- ci is the amount concentration of the attenuating species i in the material sample;
- ℓ is the path length of the beam of light through the material sample.
Attenuation cross section and molar attenuation coefficient are related by
and number density and amount concentration by
where NA is the Avogadro constant.
In case of uniform attenuation, these relations become[4]
or equivalently
Cases of non-uniform attenuation occur in atmospheric science applications and radiation shielding theory for instance.
Other radiometric coefficients
edit| Quantity | SI units | Notes | |
|---|---|---|---|
| Name | Sym. | ||
| Hemispherical emissivity | ε | — | Radiant exitance of a surface, divided by that of a black body at the same temperature as that surface. |
| Spectral hemispherical emissivity | εν ελ |
— | Spectral exitance of a surface, divided by that of a black body at the same temperature as that surface. |
| Directional emissivity | εΩ | — | Radiance emitted by a surface, divided by that emitted by a black body at the same temperature as that surface. |
| Spectral directional emissivity | εΩ,ν εΩ,λ |
— | Spectral radiance emitted by a surface, divided by that of a black body at the same temperature as that surface. |
| Hemispherical absorptance | A | — | Radiant flux absorbed by a surface, divided by that received by that surface. This should not be confused with "absorbance". |
| Spectral hemispherical absorptance | Aν Aλ |
— | Spectral flux absorbed by a surface, divided by that received by that surface. This should not be confused with "spectral absorbance". |
| Directional absorptance | AΩ | — | Radiance absorbed by a surface, divided by the radiance incident onto that surface. This should not be confused with "absorbance". |
| Spectral directional absorptance | AΩ,ν AΩ,λ |
— | Spectral radiance absorbed by a surface, divided by the spectral radiance incident onto that surface. This should not be confused with "spectral absorbance". |
| Hemispherical reflectance | R | — | Radiant flux reflected by a surface, divided by that received by that surface. |
| Spectral hemispherical reflectance | Rν Rλ |
— | Spectral flux reflected by a surface, divided by that received by that surface. |
| Directional reflectance | RΩ | — | Radiance reflected by a surface, divided by that received by that surface. |
| Spectral directional reflectance | RΩ,ν RΩ,λ |
— | Spectral radiance reflected by a surface, divided by that received by that surface. |
| Hemispherical transmittance | T | — | Radiant flux transmitted by a surface, divided by that received by that surface. |
| Spectral hemispherical transmittance | Tν Tλ |
— | Spectral flux transmitted by a surface, divided by that received by that surface. |
| Directional transmittance | TΩ | — | Radiance transmitted by a surface, divided by that received by that surface. |
| Spectral directional transmittance | TΩ,ν TΩ,λ |
— | Spectral radiance transmitted by a surface, divided by that received by that surface. |
| Hemispherical attenuation coefficient | μ | m−1 | Radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume. |
| Spectral hemispherical attenuation coefficient | μν μλ |
m−1 | Spectral radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume. |
| Directional attenuation coefficient | μΩ | m−1 | Radiance absorbed and scattered by a volume per unit length, divided by that received by that volume. |
| Spectral directional attenuation coefficient | μΩ,ν μΩ,λ |
m−1 | Spectral radiance absorbed and scattered by a volume per unit length, divided by that received by that volume. |
See also
editReferences
edit- ^ "Electronic warfare and radar systems engineering handbook". Archived from the original on September 13, 2001.
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Transmittance". doi:10.1351/goldbook.T06484
- ^ a b c d "Thermal insulation — Heat transfer by radiation — Physical quantities and definitions". ISO 9288:1989. ISO catalogue. 1989. Retrieved 2015-03-15.
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Beer–Lambert law". doi:10.1351/goldbook.B00626