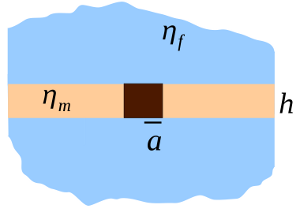
The Saffman–Delbrück model describes a lipid membrane as a thin layer of viscous fluid, surrounded by a less viscous bulk liquid. This picture was originally proposed to determine the diffusion coefficient of membrane proteins, but has also been used to describe the dynamics of fluid domains within lipid membranes. The Saffman–Delbrück formula is often applied to determine the size of an object embedded in a membrane from its observed diffusion coefficient, and is characterized by the weak logarithmic dependence of diffusion constant on object radius.
Origin
editIn a three-dimensional highly viscous liquid, a spherical object of radius a has diffusion coefficient
by the well-known Stokes–Einstein relation. By contrast, the diffusion coefficient of a circular object embedded in a two-dimensional fluid diverges; this is Stokes' paradox. In a real lipid membrane, the diffusion coefficient may be limited by:
- the size of the membrane
- the inertia of the membrane (finite Reynolds number)
- the effect of the liquid surrounding the membrane
Philip Saffman and Max Delbrück calculated the diffusion coefficient for these three cases, and showed that Case 3 was the relevant effect.[1]
Saffman–Delbrück formula
editThe diffusion coefficient of a cylindrical inclusion of radius in a membrane with thickness and viscosity , surrounded by bulk fluid with viscosity is:
where the Saffman–Delbrück length and is the Euler–Mascheroni constant. Typical values of are 0.1 to 10 micrometres.[2] This result is an approximation applicable for radii , which is appropriate for proteins ( nm), but not for micrometre-scale lipid domains.
The Saffman–Delbrück formula predicts that diffusion coefficients will only depend weakly on the size of the embedded object; for example, if , changing from 1 nm to 10 nm only reduces the diffusion coefficient by 30%.
Beyond the Saffman–Delbrück length
editHughes, Pailthorpe, and White extended the theory of Saffman and Delbrück to inclusions with any radii ;[3] for ,
A useful formula that produces the correct diffusion coefficients between these two limits is [2]
where , , , , and . Please note that the original version of [2] has a typo in ; the value in the correction[4] to that article should be used.
Experimental studies
editThough the Saffman–Delbruck formula is commonly used to infer the sizes of nanometer-scale objects, recent controversial[5] experiments on proteins have suggested that the diffusion coefficient's dependence on radius should be instead of .[6] However, for larger objects (such as micrometre-scale lipid domains), the Saffman–Delbruck model (with the extensions above) is well-established [2][7][8]
Extending Saffman–Delbrück for Hydrodynamic Coupling of Proteins within Curved Lipid Bilayer Membranes
editThe Saffman–Delbrück approach has also been extended in recent works for modeling hydrodynamic interactions between proteins embedded within curved lipid bilayer membranes, such as in vesicles and other structures.[9][10][11][12] These works use related formulations to study the roles of the membrane hydrodynamic coupling and curvature in the collective drift-diffusion dynamics of proteins within bilayer membranes. Various models of the protein inclusions within curved membranes have been developed, including models based on series truncations,[9] immersed boundary methods,[11] and fluctuating hydrodynamics.[12]
References
edit- ^ P. G. Saffman and M. Delbrück, Brownian motion in biological membranes, Proc. Natl. Acad. Sci. USA, vol. 72 p. 3111–3113 1975
- ^ a b c d Petrov, EP; Schwille, P (2008). "Translational diffusion in lipid membranes beyond the Saffman-Delbruck approximation". Biophys J. 94 (5): L41-3. Bibcode:2008BpJ....94L..41P. doi:10.1529/biophysj.107.126565. PMC 2242757. PMID 18192354.
- ^ Hughes, B.D.; Pailthorpe, B.A.; White, L.R. (1981). "The translational and rotational drag on a cylinder moving in a membrane". J. Fluid Mech. 110: 349–372. Bibcode:1981JFM...110..349H. doi:10.1017/S0022112081000785. S2CID 119749264.
- ^ Petrov; Schwille (Jul 2012). "Correction: Translational Diffusion in Lipid Membranes beyond the Saffman-Delbrück Approximation". Biophys. J. 103 (2): 375. Bibcode:2012BpJ...103..375P. doi:10.1016/j.bpj.2012.06.032. PMC 3400766.
- ^ Weiß; et al. (2013). "Quantifying the Diffusion of Membrane Proteins and Peptides in Black Lipid Membranes with 2-Focus Fluorescence Correlation Spectroscopy". Biophys. J. 105 (2): 455–462. Bibcode:2013BpJ...105..455W. doi:10.1016/j.bpj.2013.06.004. PMC 3714877. PMID 23870266.
- ^ Gambin, Y.; et al. (2006). "Lateral mobility of proteins in liquid membranes revisited". Proc. Natl. Acad. Sci. USA. 103 (7): 2098–2102. Bibcode:2006PNAS..103.2098G. doi:10.1073/pnas.0511026103. PMC 1413751. PMID 16461891.
- ^ Klingler, J.F.; McConnell, H.M. (1993). "Brownian motion and fluid mechanics of lipid monolayer domains". J. Phys. Chem. 93 (22): 6096–6100. doi:10.1021/j100124a052.
- ^ Cicuta, P.; Veatch, S.L.; Keller, S.L. (2007). "Diffusion of Liquid Domains in Lipid Bilayer Membranes". J. Phys. Chem. B. 111 (13): 3328–3331. arXiv:cond-mat/0611492. doi:10.1021/jp0702088. PMID 17388499. S2CID 46592939.
- ^ a b Henle, Mark L.; Levine, Alex J. (12 January 2010). "Hydrodynamics in curved membranes: The effect of geometry on particulate mobility". Physical Review E. 81 (1): 011905. doi:10.1103/PhysRevE.81.011905.
- ^ Daniels, D. R. (October 2016). "Curvature correction to the mobility of fluid membrane inclusions". The European Physical Journal E. 39 (10): 96. doi:10.1140/epje/i2016-16096-3.
- ^ a b Sigurdsson, Jon Karl; Atzberger, Paul J. (2016). "Hydrodynamic coupling of particle inclusions embedded in curved lipid bilayer membranes". Soft Matter. 12 (32): 6685–6707. arXiv:1601.06461. doi:10.1039/C6SM00194G.
- ^ a b Rower, David A.; Padidar, Misha; Atzberger, Paul J. (15 April 2022). "Surface fluctuating hydrodynamics methods for the drift-diffusion dynamics of particles and microstructures within curved fluid interfaces". Journal of Computational Physics. 455: 110994. arXiv:1906.01146. doi:10.1016/j.jcp.2022.110994.



