In discrete geometry, the original orchard-planting problem (or the tree-planting problem) asks for the maximum number of 3-point lines attainable by a configuration of a specific number of points in the plane. There are also investigations into how many k-point lines there can be. Hallard T. Croft and Paul Erdős proved where n is the number of points and tk is the number of k-point lines.[1] Their construction contains some m-point lines, where m > k. One can also ask the question if these are not allowed.
Integer sequence
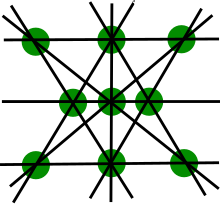
editDefine to be the maximum number of 3-point lines attainable with a configuration of n points. For an arbitrary number of n points, was shown to be in 1974.
The first few values of are given in the following table (sequence A003035 in the OEIS).
| n | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| | 1 | 2 | 4 | 6 | 7 | 10 | 12 | 16 | 19 | 22 | 26 |
Upper and lower bounds
editSince no two lines may share two distinct points, a trivial upper-bound for the number of 3-point lines determined by n points is Using the fact that the number of 2-point lines is at least (Csima & Sawyer 1993), this upper bound can be lowered to
Lower bounds for are given by constructions for sets of points with many 3-point lines. The earliest quadratic lower bound of was given by Sylvester, who placed n points on the cubic curve y = x3. This was improved to in 1974 by Burr, Grünbaum, and Sloane (1974), using a construction based on Weierstrass's elliptic functions. An elementary construction using hypocycloids was found by Füredi & Palásti (1984) achieving the same lower bound.
In September 2013, Ben Green and Terence Tao published a paper in which they prove that for all point sets of sufficient size, n > n0, there are at most 3-point lines which matches the lower bound established by Burr, Grünbaum and Sloane.[2] Thus, for sufficiently large n, the exact value of is known.
This is slightly better than the bound that would directly follow from their tight lower bound of for the number of 2-point lines: proved in the same paper and solving a 1951 problem posed independently by Gabriel Andrew Dirac and Theodore Motzkin.
Orchard-planting problem has also been considered over finite fields. In this version of the problem, the n points lie in a projective plane defined over a finite field. (Padmanabhan & Shukla 2020).
Notes
edit- ^ The Handbook of Combinatorics, edited by László Lovász, Ron Graham, et al, in the chapter titled Extremal Problems in Combinatorial Geometry by Paul Erdős and George B. Purdy.
- ^ Green & Tao (2013)
References
edit- Brass, P.; Moser, W. O. J.; Pach, J. (2005), Research Problems in Discrete Geometry, Springer-Verlag, ISBN 0-387-23815-8.
- Burr, S. A.; Grünbaum, B.; Sloane, N. J. A. (1974), "The Orchard problem", Geometriae Dedicata, 2 (4): 397–424, doi:10.1007/BF00147569, S2CID 120906839.
- Csima, J.; Sawyer, E. (1993), "There exist 6n/13 ordinary points", Discrete and Computational Geometry, 9 (2): 187–202, doi:10.1007/BF02189318.
- Füredi, Z.; Palásti, I. (1984), "Arrangements of lines with a large number of triangles", Proceedings of the American Mathematical Society, 92 (4): 561–566, doi:10.2307/2045427, JSTOR 2045427.
- Green, Ben; Tao, Terence (2013), "On sets defining few ordinary lines", Discrete and Computational Geometry, 50 (2): 409–468, arXiv:1208.4714, doi:10.1007/s00454-013-9518-9, S2CID 15813230
- Padmanabhan, R.; Shukla, Alok (2020), "Orchards in elliptic curves over finite fields", Finite Fields and Their Applications, 68 (2): 101756, arXiv:2003.07172, doi:10.1016/j.ffa.2020.101756, S2CID 212725631
