In combinatorics and order theory, a multitree may describe either of two equivalent structures: a directed acyclic graph (DAG) in which there is at most one directed path between any two vertices, or equivalently in which the subgraph reachable from any vertex induces an undirected tree, or a partially ordered set (poset) that does not have four items a, b, c, and d forming a diamond suborder with a ≤ b ≤ d and a ≤ c ≤ d but with b and c incomparable to each other (also called a diamond-free poset[1]).
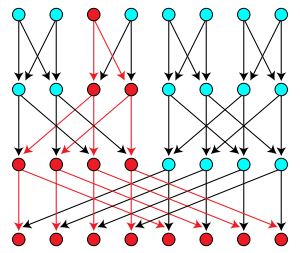
In computational complexity theory, multitrees have also been called strongly unambiguous graphs or mangroves; they can be used to model nondeterministic algorithms in which there is at most one computational path connecting any two states.[2]
Multitrees may be used to represent multiple overlapping taxonomies over the same ground set.[3] If a family tree may contain multiple marriages from one family to another, but does not contain marriages between any two blood relatives, then it forms a multitree.[4]
Equivalence between DAG and poset definitions
editIn a directed acyclic graph, if there is at most one directed path between any two vertices, or equivalently if the subgraph reachable from any vertex induces an undirected tree, then its reachability relation is a diamond-free partial order. Conversely, in a diamond-free partial order, the transitive reduction identifies a directed acyclic graph in which the subgraph reachable from any vertex induces an undirected tree.
Diamond-free families
editA diamond-free family of sets is a family F of sets whose inclusion ordering forms a diamond-free poset. If D(n) denotes the largest possible diamond-free family of subsets of an n-element set, then it is known that
- ,
and it is conjectured that the limit is 2.[1]
Related structures
editA polytree, a directed acyclic graph formed by orienting the edges of an undirected tree, is a special case of a multitree.
The subgraph reachable from any vertex in a multitree is an arborescence rooted in the vertex, that is a polytree in which all edges are oriented away from the root.
The word "multitree" has also been used to refer to a series–parallel partial order,[5] or to other structures formed by combining multiple trees.
References
edit- ^ a b Griggs, Jerrold R.; Li, Wei-Tian; Lu, Linyuan (2010), Diamond-free families, arXiv:1010.5311, Bibcode:2010arXiv1010.5311G.
- ^ Allender, Eric; Lange, Klaus-Jörn (1996), "StUSPACE(log n) ⊆ DSPACE(log2 n/log log n)", Algorithms and Computation, 7th International Symposium, ISAAC '96, Osaka, Japan, December 16–18, 1996, Proceedings, Lecture Notes in Computer Science, vol. 1178, Springer-Verlag, pp. 193–202, doi:10.1007/BFb0009495.
- ^ Furnas, George W.; Zacks, Jeff (1994), "Multitrees: enriching and reusing hierarchical structure", Proc. SIGCHI conference on Human Factors in Computing Systems (CHI '94), pp. 330–336, doi:10.1145/191666.191778, S2CID 18710118.
- ^ McGuffin, Michael J.; Balakrishnan, Ravin (2005), "Interactive visualization of genealogical graphs", IEEE Symposium on Information Visualization, Los Alamitos, California, US: IEEE Computer Society, p. 3, doi:10.1109/INFOVIS.2005.22, S2CID 15449409.
- ^ Jung, H. A. (1978), "On a class of posets and the corresponding comparability graphs", Journal of Combinatorial Theory, Series B, 24 (2): 125–133, doi:10.1016/0095-8956(78)90013-8, MR 0491356.