K-set (geometry)

In discrete geometry, a $k$-set of a finite point set $S$ in the Euclidean plane is a subset of $k$ elements of $S$ that can be strictly separated from the remaining points by a line. More generally, in Euclidean space of higher dimensions, a $k$-set of a finite point set is a subset of $k$ elements that can be separated from the remaining points by a hyperplane. In particular, when $k=n/2$ (where $n$ is the size of $S$), the line or hyperplane that separates a $k$-set from the rest of $S$ is a halving line or halving plane.

A set of six points (red), its six 2-sets (the sets of points contained in the blue ovals), and lines separating each $k$-set from the remaining points (dashed black).

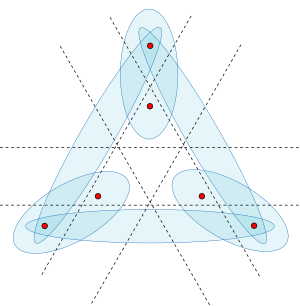
The $k$-sets of a set of points in the plane are related by projective duality to the $k$-levels in an arrangement of lines. The $k$-level in an arrangement of $n$ lines in the plane is the curve consisting of the points that lie on one of the lines and have exactly $k$ lines below them. Discrete and computational geometers have also studied levels in arrangements of more general kinds of curves and surfaces.

Combinatorial bounds

Unsolved problem in mathematics:

What is the largest possible number of halving lines for a set of $n$ points in the plane?

(more unsolved problems in mathematics)

It is of importance in the analysis of geometric algorithms to bound the number of $k$-sets of a planar point set, or equivalently the number of $k$-levels of a planar line arrangement, a problem first studied by Lovász and Erdős et al. The best known upper bound for this problem is $O(nk^{1/3})$, as was shown by Tamal Dey using the crossing number inequality of Ajtai, Chvátal, Newborn, and Szemerédi. However, the best known lower bound is far from Dey's upper bound: it is ${\textstyle \Omega (nc^{\sqrt {\log k}})}$ for some constant $c$, as shown by Tóth.

In three dimensions, the best upper bound known is $O(nk^{3/2})$, and the best lower bound known is ${\textstyle \Omega (nkc^{\sqrt {\log k}})}$. For points in three dimensions that are in convex position, that is, are the vertices of some convex polytope, the number of $k$-sets is $\Theta {\bigl (}(n-k)k{\bigr )}$, which follows from arguments used for bounding the complexity of $k$th order Voronoi diagrams.

For the case when $k=n/2$ (halving lines), the maximum number of combinatorially distinct lines through two points of $S$ that bisect the remaining points when $k=1,2,\dots$ is

1,3,6,9,13,18,22... (sequence A076523 in the OEIS).

Bounds have also been proven on the number of $\leq k$-sets, where a $\leq k$-set is a $j$-set for some $j\leq k$. In two dimensions, the maximum number of $\leq k$-sets is exactly $nk$, while in $d$ dimensions the bound is $O(n^{\lfloor d/2\rfloor }k^{\lceil d/2\rceil })$.

Construction algorithms

Edelsbrunner and Welzl first studied the problem of constructing all $k$-sets of an input point set, or dually of constructing the $k$-level of an arrangement. The $k$-level version of their algorithm can be viewed as a plane sweep algorithm that constructs the level in left-to-right order. Viewed in terms of $k$-sets of point sets, their algorithm maintains a dynamic convex hull for the points on each side of a separating line, repeatedly finds a bitangent of these two hulls, and moves each of the two points of tangency to the opposite hull. Chan surveys subsequent results on this problem, and shows that it can be solved in time proportional to Dey's $O(nk^{1/3})$ bound on the complexity of the $k$-level.

Agarwal and Matoušek describe algorithms for efficiently constructing an approximate level; that is, a curve that passes between the $(k-\delta )$-level and the $(k+\delta )$-level for some small approximation parameter $\delta$. They show that such an approximation can be found, consisting of a number of line segments that depends only on $n/\delta$ and not on $n$ or $k$.

Matroid generalizations

The planar $k$-level problem can be generalized to one of parametric optimization in a matroid: one is given a matroid in which each element is weighted by a linear function of a parameter $\lambda$, and must find the minimum weight basis of the matroid for each possible value of $\lambda$. If one graphs the weight functions as lines in a plane, the $k$-level of the arrangement of these lines graphs as a function of $\lambda$ the weight of the largest element in an optimal basis in a uniform matroid, and Dey showed that his $O(nk^{1/3})$ bound on the complexity of the $k$-level could be generalized to count the number of distinct optimal bases of any matroid with $n$ elements and rank $k$.

For instance, the same $O(nk^{1/3})$ upper bound holds for counting the number of different minimum spanning trees formed in a graph with $n$ edges and $k$ vertices, when the edges have weights that vary linearly with a parameter $\lambda$. This parametric minimum spanning tree problem has been studied by various authors and can be used to solve other bicriterion spanning tree optimization problems.

However, the best known lower bound for the parametric minimum spanning tree problem is $\Omega (n\log k)$, a weaker bound than that for the $k$-set problem. For more general matroids, Dey's $O(nk^{1/3})$ upper bound has a matching lower bound.

References

• Agarwal, P. K. (1990). "Partitioning arrangements of lines I: An efficient deterministic algorithm". Discrete & Computational Geometry. 5 (1): 449–483. doi:10.1007/BF02187805.
• Agarwal, P. K.; Aronov, B.; Sharir, M. (1997). "On levels in arrangements of lines, segments, planes, and triangles". Proc. 13th Annual Symposium on Computational Geometry. pp. 30–38.
• Alon, N.; Győri, E. (1986). "The number of small semi-spaces of a finite set of points in the plane". Journal of Combinatorial Theory. Series A. 41: 154–157. doi:10.1016/0097-3165(86)90122-6.
• Chan, T. M. (1999). "Remarks on k-level algorithms in the plane". Archived from the original on 2010-11-04.
• Chan, T. M. (2003). "On levels in arrangements of curves". Discrete & Computational Geometry. 29 (3): 375–393. doi:10.1007/s00454-002-2840-2.
• Chan, T. M. (2005a). "On levels in arrangements of curves, II: a simple inequality and its consequence". Discrete & Computational Geometry. 34: 11–24. doi:10.1007/s00454-005-1165-3.
• Chan, T. M. (2005b). "On levels in arrangements of surfaces in three dimensions". Proceedings of the 16th Annual ACM-SIAM Symposium on Discrete Algorithms. pp. 232–240.
• Chan, T. M. (2005c). "Finding the shortest bottleneck edge in a parametric minimum spanning tree". Proceedings of the 16th Annual ACM-SIAM Symposium on Discrete Algorithms. pp. 232–240.
• Chazelle, B.; Preparata, F. P. (1986). "Halfspace range search: an algorithmic application of k-sets". Discrete & Computational Geometry. 1 (1): 83–93. doi:10.1007/BF02187685. MR 0824110.
• Clarkson, K. L.; Shor, P. (1989). "Applications of random sampling, II". Discrete & Computational Geometry. 4: 387–421. doi:10.1007/BF02187740.
• Cole, R.; Sharir, M.; Yap, C. K. (1987). "On k-hulls and related problems". SIAM Journal on Computing. 16 (1): 61–77. doi:10.1137/0216005. MR 0873250.
• Dey, T. K. (1998). "Improved bounds for planar k-sets and related problems". Discrete & Computational Geometry. 19 (3): 373–382. doi:10.1007/PL00009354. MR 1608878.
• Edelsbrunner, H.; Welzl, E. (1986). "Constructing belts in two-dimensional arrangements with applications". SIAM Journal on Computing. 15 (1): 271–284. doi:10.1137/0215019.
• Eppstein, D. (1998). "Geometric lower bounds for parametric matroid optimization" (PDF). Discrete & Computational Geometry. 20 (4): 463–476. doi:10.1007/PL00009396.
• Eppstein, David (August 2022). "A stronger lower bound on parametric minimum spanning trees". Algorithmica. 85 (6): 1738–1753. arXiv:2105.05371. doi:10.1007/s00453-022-01024-9.
• Erdős, P.; Lovász, L.; Simmons, A.; Straus, E. G. (1973). "Dissection graphs of planar point sets". A Survey of Combinatorial Theory (Proc. Internat. Sympos., Colorado State Univ., Fort Collins, Colo., 1971). Amsterdam: North-Holland. pp. 139–149. MR 0363986.
• Fernández-Baca, D.; Slutzki, G.; Eppstein, D. (1996). "Using sparsification for parametric minimum spanning tree problems". Nordic Journal of Computing. 3 (4): 352–366.
• Gusfield, D. (1980). Sensitivity analysis for combinatorial optimization. Tech. Rep. UCB/ERL M80/22. University of California, Berkeley.
• Hassin, R.; Tamir, A. (1989). "Maximizing classes of two-parametric objectives over matroids". Mathematics of Operations Research. 14 (2): 362–375. doi:10.1287/moor.14.2.362.
• Ishii, H.; Shiode, S.; Nishida, T. (1981). "Stochastic spanning tree problem". Discrete Applied Mathematics. 3 (4): 263–273. doi:10.1016/0166-218X(81)90004-4.
• Katoh, N.; Ibaraki, T. (1983). On the total number of pivots required for certain parametric combinatorial optimization problems. Working Paper 71. Inst. Econ. Res., Kobe Univ. of Commerce.
• Lee, Der-Tsai (1982). "On k-nearest neighbor Voronoi diagrams in the plane". IEEE Transactions on Computers. 31 (6): 478–487. doi:10.1109/TC.1982.1676031.
• Lovász, L. (1971). "On the number of halving lines". Annales Universitatis Scientiarum Budapestinensis de Rolando Eőtvős Nominatae Sectio Mathematica. 14: 107–108.
• Matoušek, J. (1990). "Construction of ε-nets". Discrete & Computational Geometry. 5 (5): 427–448. doi:10.1007/BF02187804. MR 1064574.
• Matoušek, J. (1991). "Approximate levels in line arrangements". SIAM Journal on Computing. 20 (2): 222–227. doi:10.1137/0220013.
• Sharir, M.; Smorodinsky, S.; Tardos, G. (2001). "An improved bound for k-sets in three dimensions". Discrete & Computational Geometry. 26 (2): 195–204. doi:10.1007/s00454-001-0005-3.
• Tóth, G. (2001). "Point sets with many k-sets". Discrete & Computational Geometry. 26 (2): 187–194. doi:10.1007/s004540010022.

External links

• Halving lines and k-sets, Jeff Erickson
• The Open Problems Project, Problem 7: k-sets