In geometry, a Devil's curve, also known as the Devil on Two Sticks, is a curve defined in the Cartesian plane by an equation of the form[1]

The polar equation of this curve is of the form
Devil's curves were discovered in 1750 by Gabriel Cramer, who studied them extensively.[2]
The name comes from the shape its central lemniscate takes when graphed. The shape is named after the juggling game diabolo, which was named after the Devil[3] and which involves two sticks, a string, and a spinning prop in the likeness of the lemniscate.[4]
For , the central lemniscate, often called hourglass, is horizontal. For it is vertical. If , the shape becomes a circle. The vertical hourglass intersects the y-axis at . The horizontal hourglass intersects the x-axis at .
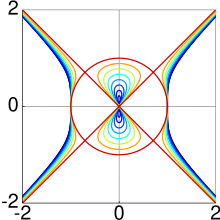
Electric Motor Curve
editA special case of the Devil's curve occurs at , where the curve is called the electric motor curve.[5] It is defined by an equation of the form
The name of the special case comes from the middle shape's resemblance to the coils of wire, which rotate from forces exerted by magnets surrounding it.
References
edit- ^ "Devil's Curve". Wolfram MathWorld.
- ^ Introduction a l'analyse des lignes courbes algébriques, p. 19 (Genova, 1750).
- ^ "Diabolo Patent". Retrieved 16 July 2013.
- ^ Wassenaar, Jan. "devil's curve". www.2dcurves.com. Retrieved 2018-02-26.
- ^ Mathematical Models, p. 71 (Cundy and Rollet. 1961)







