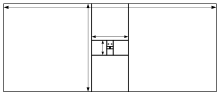
In mathematics, the silver ratio is a geometrical proportion close to 70/29. Its exact value is 1 + √2, the positive solution of the equation x2 = 2x + 1.
The name silver ratio results from analogy with the golden ratio, the positive solution of the equation x2 = x + 1.
Although its name is recent, the silver ratio (or silver mean) has been studied since ancient times because of its connections to the square root of 2, almost-isosceles Pythagorean triples, square triangular numbers, Pell numbers, the octagon, and six polyhedra with octahedral symmetry.

Definition
editIf the ratio of two quantities a > b > 0 is proportionate to the sum of two and their reciprocal ratio, they are in the silver ratio: The ratio is here denoted [a]
Based on this definition, one has
It follows that the silver ratio is found as the positive solution of the quadratic equation The quadratic formula gives the two solutions the decimal expansion of the positive root begins as (sequence A014176 in the OEIS).
Using the tangent function
or the hyperbolic sine
is the superstable fixed point of the iteration
The iteration results in the continued radical
Properties
editThe defining equation can be written
The silver ratio can be expressed in terms of itself as fractions
Similarly as the infinite geometric series
For every integer one has From this an infinite number of further relations can be found.
Continued fraction pattern of a few low powers
The silver ratio is a Pisot number,[5] the next quadratic Pisot number after the golden ratio. By definition of these numbers, the absolute value of the algebraic conjugate is smaller than 1, thus powers of generate almost integers and the sequence is dense at the borders of the unit interval.[6]
is the fundamental unit of real quadratic field
If the general quadratic equation with integer n > 0 is written as it follows by repeated substitution that all positive solutions have a purely periodic continued fraction expansion Vera de Spinadel described the properties of these irrationals and introduced the moniker metallic means.[3]
Pell sequences
editThese numbers are related to the silver ratio as the Fibonacci numbers and Lucas numbers are to the golden ratio.
The fundamental sequence is defined by the recurrence relation with initial values
The first few terms are 0, 1, 2, 5, 12, 29, 70, 169,... (sequence A000129 in the OEIS). The limit ratio of consecutive terms is the silver mean.
Fractions of Pell numbers provide rational approximations of with error
The sequence is extended to negative indices using
Powers of can be written with Pell numbers as linear coefficients which is proved by mathematical induction on n. The relation also holds for n < 0.
The generating function of the sequence is given by
The characteristic equation of the recurrence is with discriminant If the two solutions are silver ratio and conjugate so that the Pell numbers are computed with the Binet formula
- with the positive root of
Since the number is the nearest integer to with and n ≥ 0.
The Binet formula defines the companion sequence
The first few terms are 2, 2, 6, 14, 34, 82, 198,... (sequence A002203 in the OEIS).
This Pell-Lucas sequence has the Fermat property: if p is prime, The converse does not hold, the least odd pseudoprimes are 132, 385, 312, 1105, 1121, 3827, 4901.[8] [b]
Pell numbers are obtained as integral powers n > 2 of a matrix with positive eigenvalue
The trace of gives the above
Geometry
editSilver rectangle and regular octagon
editA rectangle with edges in ratio √2 ∶ 1 can be created from a square piece of paper with an origami folding sequence. Considered a proportion of great harmony in Japanese aesthetics — Yamato-hi (大和比) — the ratio is retained if the √2 rectangle is folded in half, parallel to the short edges. Rabatment produces a rectangle with edges in the silver ratio (according to 1/σ = √2 − 1). [c]
- Fold a square sheet of paper in half, creating a falling diagonal crease (bisect 90° angle), then unfold.
- Fold the right hand edge onto the diagonal crease (bisect 45° angle).
- Fold the top edge in half, to the back side (reduce width by 1/σ + 1), and open out the triangle. The result is a √2 rectangle.
- Fold the bottom edge onto the left hand edge (reduce height by 1/σ − 1). The horizontal part on top is a silver rectangle.
If the folding paper is opened out, the creases coincide with diagonal sections of a regular octagon. The first two creases divide the square into a silver gnomon with angles in the ratios 5 ∶ 2 ∶ 1, between two right triangles with angles in ratios 4 ∶ 2 ∶ 2 (left) and 4 ∶ 3 ∶ 1 (right). The unit angle is equal to 22+1/2 degrees.
If the octagon has edge length its area is and the diagonals have lengths and The coordinates of the vertices are given by the 8 permutations of [11] The paper square has edge length and area The triangles have areas and the rectangles have areas
Silver whirl
editDivide a rectangle with sides in ratio 1 ∶ 2 into four congruent right triangles with legs of equal length and arrange these in the shape of a silver rectangle, enclosing a similar rectangle that is scaled by factor and rotated about the centre by Repeating the construction at successively smaller scales results in four infinite sequences of adjoining right triangles, tracing a whirl of converging silver rectangles.[12]
The logarithmic spiral through the vertices of adjacent triangles has polar slope The parallelogram between the pair of grey triangles on the sides has perpendicular diagonals in ratio , hence is a silver rhombus.
If the triangles have legs of length then each discrete spiral has length The areas of the triangles in each spiral region sum to the perimeters are equal to (light grey) and (silver regions).
Arranging the tiles with the four hypotenuses facing inward results in the diamond-in-a-square shape. Roman architect Vitruvius recommended the implied ad quadratura ratio as one of three for proportioning a town house atrium. The scaling factor is and iteration on edge length 2 gives an angular spiral of length
Polyhedra
editThe silver mean has connections to the following Archimedean solids with octahedral symmetry; all values are based on edge length = 2.
The coordinates of the vertices are given by 24 distinct permutations of thus three mutually-perpendicular silver rectangles touch six of its square faces.
The midradius is the centre radius for the square faces is [13]
Coordinates: 24 permutations of
Midradius: centre radius for the octagon faces: [14]
Coordinates: 48 permutations of
Midradius: centre radius for the square faces: for the octagon faces: [15]
See also the dual Catalan solids
Silver triangle
editThe acute isosceles triangle formed by connecting two adjacent vertices of a regular octagon to its centre point, is here called the silver triangle. It is uniquely identified by its angles in ratios The apex angle measures each base angle degrees. It follows that the height to base ratio is
By trisecting one of its base angles, the silver triangle is partitioned into a similar triangle and an obtuse silver gnomon. The trisector coincides with a medium diagonal of the octagon. With one base angle the apex of the parent triangle, the gnomon has angles of degrees in the ratios From the law of sines, its edges are in ratios
The similar silver triangle is likewise obtained by scaling the parent triangle in base to leg ratio , accompanied with an degree rotation. Repeating the process at decreasing scales results in an infinite sequence of silver triangles, which converges at the centre of rotation. It is assumed without proof that the centre of rotation is the intersection point of sequential median lines that join corresponding legs and base vertices.[16] The assumption is verified by construction, as demonstrated in the vector image.
The centre of rotation has barycentric coordinates the three whorls of stacked gnomons have areas in ratios
The logarithmic spiral through the vertices of all nested triangles has polar slope
- or an expansion rate of for every degrees of rotation.
Silver rectangle and silver triangle
editAssume a silver rectangle has been constructed as indicated above, with height 1, length and diagonal length . The triangles on the diagonal have altitudes each perpendicular foot divides the diagonal in ratio
If an horizontal line is drawn through the intersection point of the diagonal and the internal edge of a rabatment square, the parent silver rectangle and the two scaled copies along the diagonal have areas in the ratios the rectangles opposite the diagonal both have areas equal to [17]
Relative to vertex A, the coordinates of feet of altitudes U and V are
If the diagram is further subdivided by perpendicular lines through U and V, the lengths of the diagonal and its subsections can be expressed as trigonometric functions of argument degrees, the base angle of the silver triangle:
- with
Both the lengths of the diagonal sections and the trigonometric values are elements of biquadratic number field
The silver rhombus with edge has diagonal lengths equal to and The regular octagon with edge has long diagonals of length that divide it into eight silver triangles. Since the regular octagon is defined by its side length and the angles of the silver triangle, it follows that all measures can be expressed in powers of σ and the diagonal segments of the silver rectangle, as illustrated above, pars pro toto on a single triangle.
The leg to base ratio has been dubbed the Cordovan proportion by Spanish architect Rafael de la Hoz Arderius. According to his observations, it is a notable measure in the architecture and intricate decorations of the mediæval Mosque of Córdoba, Andalusia.[18]
Silver spiral
editA silver spiral is a logarithmic spiral that gets wider by a factor of for every quarter turn. It is described by the polar equation with initial radius and parameter If drawn on a silver rectangle, the spiral has its pole at the foot of altitude of a triangle on the diagonal and passes through vertices of paired squares which are perpendicularly aligned and successively scaled by a factor
Ammann–Beenker tiling
editThe silver ratio appears prominently in the Ammann–Beenker tiling, a non-periodic tiling of the plane with octagonal symmetry, build from a square and silver rhombus with equal side lengths. Discovered by Robert Ammann in 1977, its algebraic properties were described by Frans Beenker five years later.[19] If the squares are cut into two triangles, the inflation factor for Ammann A5-tiles is the dominant eigenvalue of substitution matrix
See also
edit- Solutions of equations similar to :
- Golden ratio – the real positive solution of the equation
- Metallic means – real positive solutions of the general equation
- Supersilver ratio – the only real solution of the equation
Notes
edit- ^ Variously T(2),[1] S2, δS,[2] σAg.[3] The last notation is adopted without the subscript, which is relevant only to the context of metallic means.
- ^ There are 3360 odd composite numbers below 109 that pass the Pell-Lucas test. This compares favourably to the number of odd Fibonacci, Pell, Lucas-Selfridge or base-2 Fermat pseudoprimes.[9]
- ^ In 1979 the British Origami Society proposed the alias silver rectangle for the √2 rectangle, which is commonly used now.[10] In this article the name is reserved for the σ rectangle.
References
edit- ^ Knott, Ron (2015). "An introduction to Continued Fractions". Dr Ron Knott's web pages on Mathematics. University of Surrey. Retrieved December 11, 2024.
- ^ Weisstein, Eric W. "Silver ratio". MathWorld.
- ^ a b Spinadel, Vera W. de (1997). New Smarandache sequences: the family of metallic means. Proceedings of the first international conference on Smarandache type notions in number theory (Craiova, Romania). Rehoboth, NM: American Research Press. pp. 79–114. doi:10.5281/ZENODO.9055.
- ^ Sloane, N. J. A. (ed.). "Sequence A014176". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Panju, Maysum (2011). "A systematic construction of almost integers" (PDF). The Waterloo Mathematics Review. 1 (2): 35–43.
- ^ Weisstein, Eric W. "Power Fractional Parts". MathWorld.
- ^ Horadam, A. F. (1971). "Pell identities". The Fibonacci Quarterly. 9 (3): 245–252, 263 [248]. doi:10.1080/00150517.1971.12431004.
- ^ Sloane, N. J. A. (ed.). "Sequence A330276". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Jacobsen, Dana (2020). "Pseudoprime statistics and tables". ntheory.org. Retrieved 18 December 2024.
- ^ Lister, David (2021). "A4 (Silver) Rectangles". The Lister List. British Origami Society. Retrieved December 15, 2024.
- ^ Kapusta, Janos (2004), "The square, the circle, and the golden proportion: a new class of geometrical constructions" (PDF), Forma, 19: 293–313
- ^ Walser, Hans (2022). Spiralen, Schraubenlinien und spiralartige Figuren (in German). Berlin, Heidelberg: Springer Spektrum. pp. 77–78. doi:10.1007/978-3-662-65132-2. ISBN 978-3-662-65131-5.
- ^ McCooey, David. "Rhombicuboctahedron". Visual Polyhedra. Retrieved 11 December 2024.
- ^ McCooey, David. "Truncated Cube". Visual Polyhedra. Retrieved 11 December 2024.
- ^ McCooey, David. "Truncated Cuboctahedron". Visual Polyhedra. Retrieved 11 December 2024.
- ^ Proved for the golden triangle in: Loeb, Arthur L.; Varney, William (1992). "Does the golden spiral exist, and if not, where is its center?". In Hargittai, István; Pickover, Clifford A. (eds.). Spiral Symmetry. Singapore: World Scientific. pp. 47–61. doi:10.1142/9789814343084_0002. ISBN 981-02-0615-1. Retrieved January 14, 2025.
- ^ Analogue to the construction in: Crilly, Tony (1994). "A supergolden rectangle". The Mathematical Gazette. 78 (483): 320–325. doi:10.2307/3620208. JSTOR 3620208.
- ^ Redondo Buitrago, Antonia; Reyes Iglesias, Encarnación (2008). "The Geometry of the Cordovan Polygons" (PDF). Visual Mathematics. 10 (4). Belgrade: Mathematical Institute. ISSN 1821-1437. Retrieved December 11, 2024.
- ^ Harriss, Edmund (2007). Images of the Ammann-Beenker Tiling (PDF). Bridges Donostia: Mathematics, music, art, architecture, culture. San Sebastián: The Bridges Organization. pp. 377–378.
External links
edit- YouTube lecture on the silver ratio, Pell sequence and metallic means
- Silver rectangle and Pell sequence at Tartapelago by Giorgio Pietrocola