Truncated tetrahedron

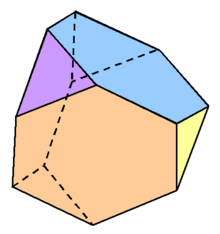
In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges (of two types). It can be constructed by truncating all 4 vertices of a regular tetrahedron.

Truncated tetrahedron
Type	Archimedean solid, Uniform polyhedron, Goldberg polyhedron
Faces	4 hexagons 4 triangles
Edges	18
Vertices	12
Symmetry group	tetrahedral symmetry $\mathrm {T} _{\mathrm {h} }$
Dual polyhedron	triakis tetrahedron
Vertex figure
Net

Construction

The truncated tetrahedron can be constructed from a regular tetrahedron by cutting all of its vertices off, a process known as truncation. The resulting polyhedron has 4 equilateral triangles and 4 regular hexagons, 18 edges, and 12 vertices. With edge length 1, the Cartesian coordinates of the 12 vertices are points

$${\bigl (}{\pm {\tfrac {3{\sqrt {2}}}{4}}},\pm {\tfrac {\sqrt {2}}{4}},\pm {\tfrac {\sqrt {2}}{4}}{\bigr )}$$

that have an even number of minus signs.

Properties

Given the edge length $a$. The surface area of a truncated tetrahedron $A$ is the sum of 4 regular hexagons and 4 equilateral triangles' area, and its volume $V$ is: $${\begin{aligned}A&=7{\sqrt {3}}a^{2}&&\approx 12.124a^{2},\\V&={\tfrac {23}{12}}{\sqrt {2}}a^{3}&&\approx 2.711a^{3}.\end{aligned}}$$

The dihedral angle of a truncated tetrahedron between triangle-to-hexagon is approximately 109.47°, and that between adjacent hexagonal faces is approximately 70.53°.

The densest packing of the truncated tetrahedron is believed to be ${\textstyle \Phi ={\frac {207}{208}}}$, as reported by two independent groups using Monte Carlo methods by Damasceno, Engel & Glotzer (2012) and Jiao & Torquato (2013). Although no mathematical proof exists that this is the best possible packing for the truncated tetrahedron, the high proximity to the unity and independence of the findings make it unlikely that an even denser packing is to be found. If the truncation of the corners is slightly smaller than that of a truncated tetrahedron, this new shape can be used to fill space completely.

3D model of a truncated tetrahedron

The truncated tetrahedron is an Archimedean solid, meaning it is a highly symmetric and semi-regular polyhedron, and two or more different regular polygonal faces meet in a vertex. The truncated tetrahedron has the same three-dimensional group symmetry as the regular tetrahedron, the tetrahedral symmetry $\mathrm {T} _{\mathrm {h} }$. The polygonal faces that meet for every vertex are one equilateral triangle and two regular hexagons, and the vertex figure is denoted as $3\cdot 6^{2}$. Its dual polyhedron is triakis tetrahedron, a Catalan solid, shares the same symmetry as the truncated tetrahedron.

Related polyhedrons

The truncated tetrahedron can be found in the construction of polyhedrons. For example, the augmented truncated tetrahedron is a Johnson solid constructed from a truncated tetrahedron by attaching triangular cupola onto its hexagonal face. The triakis truncated tetrahedron is a polyhedron constructed from a truncated tetrahedron by adding three tetrahedrons onto its triangular faces, as interpreted by the name "triakis". It is classified as plesiohedron, meaning it can tessellate in three-dimensional space known as honeycomb; an example is triakis truncated tetrahedral honeycomb.

The Friauf polyhedron is named after J. B. Friauf in which he described it as a intermetallic structure formed by a compound of metallic elements. It can be found in crystals such as complex metallic alloys, an example is dizinc magnesium MgZn₂. It is a lower symmetry version of the truncated tetrahedron, interpreted as a truncated tetragonal disphenoid with its three-dimensional symmetry group as the dihedral group $D_{2\mathrm {d} }$ of order 8.

Truncating a truncated tetrahedron gives the resulting polyhedron 54 edges, 32 vertices, and 20 faces—4 hexagons, 4 nonagons, and 12 trapeziums. This polyhedron was used by Adidas as the underlying geometry of the Jabulani ball designed for the 2010 World Cup.

Truncated tetrahedral graph

The graph of a truncated tetrahedron

In the mathematical field of graph theory, a truncated tetrahedral graph is an Archimedean graph, the graph of vertices and edges of the truncated tetrahedron, one of the Archimedean solids. It has 12 vertices and 18 edges. It is a connected cubic graph, and connected cubic transitive graph.

Examples

• 
  drawing in De divina proportione (1509)
• 
  drawing in Perspectiva Corporum Regularium (1568)
• 
  crystal model
• 
  photos from different perspectives (Matemateca)
• 
  4-sided die
• 
  12 permutations of $(4,2,0,0)$ (brown)

See also

• Quarter cubic honeycomb – Fills space using truncated tetrahedra and smaller tetrahedra
• Truncated 5-cell – Similar uniform polytope in 4-dimensions
• Truncated triakis tetrahedron
• Triakis truncated tetrahedron
• Octahedron – a rectified tetrahedron
• Truncated Triangular Pyramid Number

References

• Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press

External links

• Weisstein, Eric W., "Truncated tetrahedron" ("Archimedean solid") at MathWorld.
  • Weisstein, Eric W. "Truncated tetrahedral graph". MathWorld.
• Klitzing, Richard. "3D convex uniform polyhedra x3x3o - tut".
• Editable printable net of a truncated tetrahedron with interactive 3D view
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra