This article needs additional citations for verification. (March 2020) |
The Z-score formula for predicting bankruptcy was published in 1968 by Edward I. Altman, who was, at the time, an Assistant Professor of Finance at New York University. The formula may be used to determine the probability that a firm will go into bankruptcy within two years. Z-scores are used to predict corporate defaults and an easy-to-calculate control measure for the financial distress status of companies in academic studies. The Z-score uses multiple corporate income and balance sheet values to measure the financial health of a company.
The formula
editThe Z-score is a linear combination of four or five common business ratios, weighted by coefficients. The coefficients were estimated by identifying a set of firms which had declared bankruptcy and then collecting a matched sample of firms which had survived, with matching by industry and approximate size (assets).
Altman applied the statistical method of discriminant analysis to a dataset of publicly held manufacturers. The estimation was originally based on data from publicly held manufacturers, but has since been re-estimated based on other datasets for private manufacturing, non-manufacturing and service companies.
The original data sample consisted of 66 firms, half of which had filed for bankruptcy under Chapter 7. All businesses in the database were manufacturers, and small firms with assets of < $1 million were eliminated.
The original Z-score formula was as follows:[1]
- Z = 1.2X1 + 1.4X2 + 3.3X3 + 0.6X4 + 1.0X5.
- X1 = ratio of working capital to total assets. Measures liquid assets in relation to the size of the company.
- X2 = ratio of retained earnings to total assets. Measures profitability that reflects the company's age and earning power.
- X3 = ratio of earnings before interest and taxes to total assets. Measures operating efficiency apart from tax and leveraging factors. It recognizes operating earnings as being important to long-term viability.
- X4 = ratio of market value of equity to book value of total liabilities. Adds market dimension that can show up security price fluctuation as a possible red flag.
- X5 = ratio of sales to total assets. Standard measure for total asset turnover (varies greatly from industry to industry).
Altman found that the ratio profile for the bankrupt group fell at −0.25 avg, and for the non-bankrupt group at +4.48 avg.
Precedents
editAltman's work built upon research by accounting researcher William Beaver and others. In the 1930s and on, Mervyn[who?] and others[who?] had collected matched samples and assessed that various accounting ratios appeared to be valuable in predicting bankruptcy.[citation needed] Altman Z-score is a customized version of the discriminant analysis technique of R. A. Fisher (1936).
William Beaver's work, published in 1966 and 1968, was the first to apply a statistical method, t-tests to predict bankruptcy for a pair-matched sample of firms. Beaver applied this method to evaluate the importance of each of several accounting ratios based on univariate analysis, using each accounting ratio one at a time. Altman's primary improvement was to apply a statistical method, discriminant analysis, which could take into account multiple variables simultaneously.
Accuracy and effectiveness
editIn its initial test, the Altman Z-score was found to be 72% accurate in predicting bankruptcy two years before the event, with a Type II error (false negatives) of 6% (Altman, 1968). In a series of subsequent tests covering three periods over the next 31 years (up until 1999), the model was found to be approximately 80–90% accurate in predicting bankruptcy one year before the event, with a Type II error (classifying the firm as bankrupt when it does not go bankrupt) of approximately 15–20% (Altman, 2000).[2]
This overstates the predictive ability of the Altman Z-score, however. Scholars have long criticized the Altman Z-score for being “largely descriptive statements devoid of predictive content ... Altman demonstrates that failed and non-failed firms have dissimilar ratios, not that ratios have predictive power. But the crucial problem is to make an inference in the reverse direction, i.e., from ratios to failures.”[3] From about 1985 onwards, the Z-scores gained wide acceptance by auditors, management accountants, courts, and database systems used for loan evaluation (Eidleman). The formula's approach has been used in a variety of contexts and countries, although it was designed originally for publicly held manufacturing companies with assets of more than $1 million. Later variations by Altman were designed to be applicable to privately held companies (the Altman Z'-score) and non-manufacturing companies (the Altman Z"-score).
Neither the Altman models nor other balance sheet-based models are recommended for use with financial companies. This is because of the opacity of financial companies' balance sheets and their frequent use of off-balance sheet items.
Modern academic default and bankruptcy prediction models rely heavily on market-based data rather than the accounting ratios predominant in the Altman Z-score.[4]
Original Z-score component definitions
edit- X1 = working capital / total assets
- X2 = retained earnings / total assets
- X3 = earnings before interest and taxes / total assets
- X4 = market value of equity / total liabilities
- X5 = sales / total assets
Z-score bankruptcy model:
- Z = 1.2X1 + 1.4X2 + 3.3X3 + 0.6X4 + 1X5
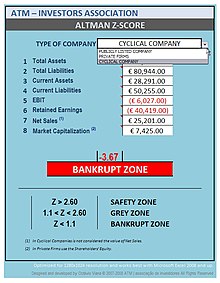
Zones of discrimination:
- Z > 2.99 – "safe" zone
- 1.81 < Z < 2.99 – "grey" zone
- Z < 1.81 – "distress" zone
Z-score estimated for non-manufacturers and emerging markets
edit- X1 = (current assets − current liabilities) / total assets
- X2 = retained earnings / total assets
- X3 = earnings before interest and taxes / total assets
- X4 = book value of equity / total liabilities
Z-score bankruptcy model (non-manufacturers):
- Z = 6.56X1 + 3.26X2 + 6.72X3 + 1.05X4[5]
Z-score bankruptcy model (emerging markets):
- Z = 3.25 + 6.56X1 + 3.26X2 + 6.72X3 + 1.05X4
Zones of discrimination:
- Z > 2.6 – "safe" zone
- 1.1 < Z < 2.6 – "grey" zone
- Z < 1.1 – "distress" zone
Examples
edit| Altman's Z-score for International Credit Rating Agencies | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Defaulter | Amount of Liabilities | Date of Default | Z-Score | Rating at the time of default | The Consequences | ||||||
| (in $ billion) | In year of default | 1 year prior | 2 years prior | 3 years prior | 4 years prior | S&P | Moody's | Fitch | |||
| Bear Stearns | 387 | 31-July-2007 | 0.29 | −0.79 | 0.45 | 0.4 | 0.36 | AA a A | A1 a A2 | Acquired by JP Morgan Chase | |
| AIG | 807 | 16-Sep-2008 | −1.03 | −0.07 | −0.02 | 0.42 | 0.23 | AA− a A− | A1 a A2 | AA− a A− | Bailed out by US Government |
| Lehman Brothers | 392 | 23-Sep-2008 | 0.06 | 0.09 | 0.03 | -0.03 | 0.29 | AA, A1 | P1 & A1 | AA− & F1+ | Bankrupt |
| Washington Mutual Bank | 303 | 25-Sep-2008 | −0.35 | −0.3 | −0.07 | −0.13 | -0.3 | A− & A2 | Baa1 & P2 | A− & F2 | Acquired by JP Morgan Chase |
| Ford Motors | 132 | 6-Apr-2009 | 1.32 | 1.03 | 1.23 | 1 | 1.29 | CC | Caa1, B3 | CCC, BB | Revived |
| MF Global | 51 | 31-Oct-2011 | 0.23 | 0.47 | 0.37 | 0.41 | 0.46 | Baa2 a Caa | BBB a BB+ | Bankrupt | |
| Altman's Z-scores of largest Indian Defaulters during April 2005 to March 2013 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Defaulter | Amount of Liabilities (in Rs cr) | Date of default | Z-Score | Rating at the time of default | The Consequences | ||||
| in Crore | In the Year of default | 1 yr prior to default | 2 yr prior to default | 3 yr prior to default | 4 yr prior to default | ||||
| Arvind Products | 251.8 | 10-Feb-2009 | 1.58 | 1.93 | 2.14 | 1.61 | 1.73 | CRSIL BBB | Restructured |
| Ansal Properties & Infraestructure | 1359 | 5-Oct-2009 | 2.3 | 3.21 | 4.22 | 4.85 | 3.06 | Fitch BBB | Restructured |
| Kingfisher Airlines Limited | 4105.88 | 1-Dec-2011 | −2.36 | 1.85 | 0.61 | 0.79 | 1.93 | CRISIL D | Non Operational |
| Royal Orchid Hotel Limited | 220 | 31-Mar-2012 | 0.77 | 1.06 | 1.17 | 1.62 | 2.17 | ICRA BBB+ | Restructured |
| Deccan Chronicle Holdings | 3902 | 2-Jul-2012 | −0.12 | 2.74 | 3.01 | 2.54 | 2.77 | Care A1 | Assets sold by banks |
| Suzlon Energy Limited | 10948 | 17-Jun-2012 | −0.11 | 1.23 | 1.28 | 1.19 | 1.24 | ICRA BBB− a D | Restructured |
See also
editReferences
editAltman, Edward I. (July 2000). "Predicting Financial Distress of Companies" (PDF). Stern.nyu.edu: 15–22.
Altman, Edward I. (September 1968). "Financial Ratios, Discriminant Analysis and the Prediction of Corporate Bankruptcy". Journal of Finance. 23 (4): 189–209. doi:10.1111/j.1540-6261.1968.tb00843.x. S2CID 154437292.
Altman, Edward I. (May 2002). "Revisiting Credit Scoring Models in a Basel II Environment" (PDF). Prepared for "Credit Rating: Methodologies, Rationale, and Default Risk", London Risk Books 2002. Archived from the original (PDF) on 2006-09-18. Retrieved 2007-08-08.
Eidleman, Gregory J. (1995-02-01). "Z-Scores – A Guide to Failure Prediction". The CPA Journal Online.
Fisher, Ronald Aylmer (1936). "The Use of Multiple Measurements in Taxonomic Problems". Annals of Eugenics. 7 (2): 179. doi:10.1111/j.1469-1809.1936.tb02137.x. hdl:2440/15227.
The Use of Credit Scoring Modules and the Importance of a Credit Culture by Dr. Edward I Altman, Stern School of Business, New York University.
- ^ realequityresearch.dk/Documents/Z-Score_Altman_1968.pdf
- ^ Predicting Financial Distress of Companies: Revisiting the Z-SCORE and ZETA Models
- ^ Johnson, C.G. 1970. Ratio Analysis and the Prediction of Firm Failure. Journal of Finance, 25(5), 1166-1168. For additional criticism, see, for example, Moyer, R.C. 1977. Forecasting Financial Failure. Financial Management, 6(1), 11-17.
- ^ See, for example, Shumway, T. 2001. Forecasting Bankruptcy More Accurately: A Simple Hazard Model. Journal of Business, 74(1), 101–124.; Campbell, J.Y., J. Hillscher, and J. Szilagyi. 2008. In Search of Distress Risk. Journal of Finance, 63(6), 2899-2939; Li, L. and R. Faff. 2019. Predicting Corporate Bankruptcy: What Matters? International Review of Economics and Finance, 62, 1–19.
- ^ Edward I. Altman; et al. (June 2017). "Financial Distress Prediction in an International Context: A Review and Empirical Analysis of Altman's Z-Score Model". Journal of International Financial Management and Accounting. 28 (2): 131–171. doi:10.1111/jifm.12053. S2CID 155302026.
- ^ a b Khatkale, Swati (2014). Symbiosis International University (ed.). "An exploratory study to assess the performance of indian credit rating agencies 2005 2013". hdl:10603/38090. Retrieved 19 December 2021.
On the other hand all the defaults in case of Indian rated companies were in non-structured financial products. Defaulters like Arvind Products, Suzlon, Royal Orchid Hotel, Deccan Chronicle Holding & Ansal Properties had investment grade ratings either at the time of default or just a few days before the default. Altman's Z score predicted default in case of Royal Orchid, Arvind Products & Suzlon Energy, which was not reflected in the ratings. This showed that simple model like Altman's Z score was more informative than the ratings given by Credit Rating Agencies. Thus the findings of the case studies support the findings of overall accuracy of Indian Credit Rating Agencies based on default rates. So Indian Credit Rating Agencies have to improve the accuracy & timeliness of the ratings of normal non structured products.
Further reading
edit- Caouette, John B; Edward I Altman, Paul Narayanan (1998). Managing Credit Risk – the Next Great Financial Challenge, John Wiley & Sons: New York. ISBN 978-0-471-11189-4
- Mare, Davide; Moreira, Fernando; Rossi, Roberto (2016). "Nonstationary Z-score measures". European Journal of Operational Research. 260: 348–358. doi:10.1016/j.ejor.2016.12.001. hdl:20.500.11820/0a77ff25-1f7c-40a0-8eb4-57f7b19ba48a. SSRN 2688367.