In mathematics, the restriction of a function is a new function, denoted or obtained by choosing a smaller domain for the original function The function is then said to extend
Formal definition
editLet be a function from a set to a set If a set is a subset of then the restriction of to is the function[1] given by for Informally, the restriction of to is the same function as but is only defined on .
If the function is thought of as a relation on the Cartesian product then the restriction of to can be represented by its graph,
where the pairs represent ordered pairs in the graph
Extensions
editA function is said to be an extension of another function if whenever is in the domain of then is also in the domain of and That is, if and
A linear extension (respectively, continuous extension, etc.) of a function is an extension of that is also a linear map (respectively, a continuous map, etc.).
Examples
edit- The restriction of the non-injective function to the domain is the injection
- The factorial function is the restriction of the gamma function to the positive integers, with the argument shifted by one:
Properties of restrictions
edit- Restricting a function to its entire domain gives back the original function, that is,
- Restricting a function twice is the same as restricting it once, that is, if then
- The restriction of the identity function on a set to a subset of is just the inclusion map from into [2]
- The restriction of a continuous function is continuous.[3][4]
Applications
editInverse functions
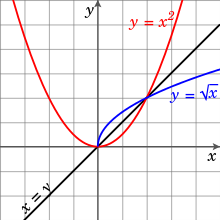
editFor a function to have an inverse, it must be one-to-one. If a function is not one-to-one, it may be possible to define a partial inverse of by restricting the domain. For example, the function defined on the whole of is not one-to-one since for any However, the function becomes one-to-one if we restrict to the domain in which case
(If we instead restrict to the domain then the inverse is the negative of the square root of ) Alternatively, there is no need to restrict the domain if we allow the inverse to be a multivalued function.
Selection operators
editIn relational algebra, a selection (sometimes called a restriction to avoid confusion with SQL's use of SELECT) is a unary operation written as or where:
- and are attribute names,
- is a binary operation in the set
- is a value constant,
- is a relation.
The selection selects all those tuples in for which holds between the and the attribute.
The selection selects all those tuples in for which holds between the attribute and the value
Thus, the selection operator restricts to a subset of the entire database.
The pasting lemma
editThe pasting lemma is a result in topology that relates the continuity of a function with the continuity of its restrictions to subsets.
Let be two closed subsets (or two open subsets) of a topological space such that and let also be a topological space. If is continuous when restricted to both and then is continuous.
This result allows one to take two continuous functions defined on closed (or open) subsets of a topological space and create a new one.
Sheaves
editSheaves provide a way of generalizing restrictions to objects besides functions.
In sheaf theory, one assigns an object in a category to each open set of a topological space, and requires that the objects satisfy certain conditions. The most important condition is that there are restriction morphisms between every pair of objects associated to nested open sets; that is, if then there is a morphism satisfying the following properties, which are designed to mimic the restriction of a function:
- For every open set of the restriction morphism is the identity morphism on
- If we have three open sets then the composite
- (Locality) If is an open covering of an open set and if are such that for each set of the covering, then ; and
- (Gluing) If is an open covering of an open set and if for each a section is given such that for each pair of the covering sets the restrictions of and agree on the overlaps: then there is a section such that for each
The collection of all such objects is called a sheaf. If only the first two properties are satisfied, it is a pre-sheaf.
Left- and right-restriction
editMore generally, the restriction (or domain restriction or left-restriction) of a binary relation between and may be defined as a relation having domain codomain and graph Similarly, one can define a right-restriction or range restriction Indeed, one could define a restriction to -ary relations, as well as to subsets understood as relations, such as ones of the Cartesian product for binary relations. These cases do not fit into the scheme of sheaves.[clarification needed]
Anti-restriction
editThe domain anti-restriction (or domain subtraction) of a function or binary relation (with domain and codomain ) by a set may be defined as ; it removes all elements of from the domain It is sometimes denoted ⩤ [5] Similarly, the range anti-restriction (or range subtraction) of a function or binary relation by a set is defined as ; it removes all elements of from the codomain It is sometimes denoted ⩥
See also
edit- Constraint – Condition of an optimization problem which the solution must satisfy
- Deformation retract – Continuous, position-preserving mapping from a topological space into a subspace
- Local property – property which occurs on sufficiently small or arbitrarily small neighborhoods of points
- Function (mathematics) § Restriction and extension
- Binary relation § Restriction
- Relational algebra § Selection (σ)
References
edit- ^ Stoll, Robert (1974). Sets, Logic and Axiomatic Theories (2nd ed.). San Francisco: W. H. Freeman and Company. pp. [36]. ISBN 0-7167-0457-9.
- ^ Halmos, Paul (1960). Naive Set Theory. Princeton, NJ: D. Van Nostrand. Reprinted by Springer-Verlag, New York, 1974. ISBN 0-387-90092-6 (Springer-Verlag edition). Reprinted by Martino Fine Books, 2011. ISBN 978-1-61427-131-4 (Paperback edition).
- ^ Munkres, James R. (2000). Topology (2nd ed.). Upper Saddle River: Prentice Hall. ISBN 0-13-181629-2.
- ^ Adams, Colin Conrad; Franzosa, Robert David (2008). Introduction to Topology: Pure and Applied. Pearson Prentice Hall. ISBN 978-0-13-184869-6.
- ^ Dunne, S. and Stoddart, Bill Unifying Theories of Programming: First International Symposium, UTP 2006, Walworth Castle, County Durham, UK, February 5–7, 2006, Revised Selected ... Computer Science and General Issues). Springer (2006)








