This article needs additional citations for verification. (January 2021) |
Protein structure prediction is the inference of the three-dimensional structure of a protein from its amino acid sequence—that is, the prediction of its secondary and tertiary structure from primary structure. Structure prediction is different from the inverse problem of protein design.
Protein structure prediction is one of the most important goals pursued by computational biology and addresses Levinthal's paradox. Accurate structure prediction has important applications in medicine (for example, in drug design) and biotechnology (for example, in novel enzyme design).
Starting in 1994, the performance of current methods is assessed biannually in the Critical Assessment of Structure Prediction (CASP) experiment. A continuous evaluation of protein structure prediction web servers is performed by the community project Continuous Automated Model EvaluatiOn (CAMEO3D).
Protein structure and terminology
editProteins are chains of amino acids joined together by peptide bonds. Many conformations of this chain are possible due to the rotation of the main chain about the two torsion angles φ and ψ at the Cα atom (see figure). This conformational flexibility is responsible for differences in the three-dimensional structure of proteins. The peptide bonds in the chain are polar, i.e. they have separated positive and negative charges (partial charges) in the carbonyl group, which can act as hydrogen bond acceptor and in the NH group, which can act as hydrogen bond donor. These groups can therefore interact in the protein structure. Proteins consist mostly of 20 different types of L-α-amino acids (the proteinogenic amino acids). These can be classified according to the chemistry of the side chain, which also plays an important structural role. Glycine takes on a special position, as it has the smallest side chain, only one hydrogen atom, and therefore can increase the local flexibility in the protein structure. Cysteine in contrast can react with another cysteine residue to form one cystine and thereby form a cross link stabilizing the whole structure.
The protein structure can be considered as a sequence of secondary structure elements, such as α helices and β sheets. In these secondary structures, regular patterns of H-bonds are formed between the main chain NH and CO groups of spatially neighboring amino acids, and the amino acids have similar Φ and ψ angles.[1]
The formation of these secondary structures efficiently satisfies the hydrogen bonding capacities of the peptide bonds. The secondary structures can be tightly packed in the protein core in a hydrophobic environment, but they can also present at the polar protein surface. Each amino acid side chain has a limited volume to occupy and a limited number of possible interactions with other nearby side chains, a situation that must be taken into account in molecular modeling and alignments.[2][3]
α-helix
editThe α-helix is the most abundant type of secondary structure in proteins. The α-helix has 3.6 amino acids per turn with an H-bond formed between every fourth residue; the average length is 10 amino acids (3 turns) or 10 Å but varies from 5 to 40 (1.5 to 11 turns). The alignment of the H-bonds creates a dipole moment for the helix with a resulting partial positive charge at the amino end of the helix. Because this region has free NH2 groups, it will interact with negatively charged groups such as phosphates. The most common location of α-helices is at the surface of protein cores, where they provide an interface with the aqueous environment. The inner-facing side of the helix tends to have hydrophobic amino acids and the outer-facing side hydrophilic amino acids. Thus, every third of four amino acids along the chain will tend to be hydrophobic, a pattern that can be quite readily detected. In the leucine zipper motif, a repeating pattern of leucines on the facing sides of two adjacent helices is highly predictive of the motif. A helical-wheel plot can be used to show this repeated pattern. Other α-helices buried in the protein core or in cellular membranes have a higher and more regular distribution of hydrophobic amino acids, and are highly predictive of such structures. Helices exposed on the surface have a lower proportion of hydrophobic amino acids. Amino acid content can be predictive of an α-helical region. Regions richer in alanine (A), glutamic acid (E), leucine (L), and methionine (M) and poorer in proline (P), glycine (G), tyrosine (Y), and serine (S) tend to form an α-helix. Proline destabilizes or breaks an α-helix but can be present in longer helices, forming a bend.
β-sheet
editβ-sheets are formed by H-bonds between an average of 5–10 consecutive amino acids in one portion of the chain with another 5–10 farther down the chain. The interacting regions may be adjacent, with a short loop in between, or far apart, with other structures in between. Every chain may run in the same direction to form a parallel sheet, every other chain may run in the reverse chemical direction to form an anti parallel sheet, or the chains may be parallel and anti parallel to form a mixed sheet. The pattern of H bonding is different in the parallel and anti parallel configurations. Each amino acid in the interior strands of the sheet forms two H-bonds with neighboring amino acids, whereas each amino acid on the outside strands forms only one bond with an interior strand. Looking across the sheet at right angles to the strands, more distant strands are rotated slightly counterclockwise to form a left-handed twist. The Cα-atoms alternate above and below the sheet in a pleated structure, and the R side groups of the amino acids alternate above and below the pleats. The Φ and Ψ angles of the amino acids in sheets vary considerably in one region of the Ramachandran plot. It is more difficult to predict the location of β-sheets than of α-helices. The situation improves somewhat when the amino acid variation in multiple sequence alignments is taken into account.
Deltas
editSome parts of the protein have fixed three-dimensional structure, but do not form any regular structures. They should not be confused with disordered or unfolded segments of proteins or random coil, an unfolded polypeptide chain lacking any fixed three-dimensional structure. These parts are frequently called "deltas" (Δ) because they connect β-sheets and α-helices. Deltas are usually located at protein surface, and therefore mutations of their residues are more easily tolerated. Having more substitutions, insertions, and deletions in a certain region of a sequence alignment maybe an indication of some delta. The positions of introns in genomic DNA may correlate with the locations of loops in the encoded protein [citation needed]. Deltas also tend to have charged and polar amino acids and are frequently a component of active sites.
Protein classification
editProteins may be classified according to both structural and sequential similarity. For structural classification, the sizes and spatial arrangements of secondary structures described in the above paragraph are compared in known three-dimensional structures. Classification based on sequence similarity was historically the first to be used. Initially, similarity based on alignments of whole sequences was performed. Later, proteins were classified on the basis of the occurrence of conserved amino acid patterns. Databases that classify proteins by one or more of these schemes are available. In considering protein classification schemes, it is important to keep several observations in mind. First, two entirely different protein sequences from different evolutionary origins may fold into a similar structure. Conversely, the sequence of an ancient gene for a given structure may have diverged considerably in different species while at the same time maintaining the same basic structural features. Recognizing any remaining sequence similarity in such cases may be a very difficult task. Second, two proteins that share a significant degree of sequence similarity either with each other or with a third sequence also share an evolutionary origin and should share some structural features also. However, gene duplication and genetic rearrangements during evolution may give rise to new gene copies, which can then evolve into proteins with new function and structure.[2]
Terms used for classifying protein structures and sequences
editThe more commonly used terms for evolutionary and structural relationships among proteins are listed below. Many additional terms are used for various kinds of structural features found in proteins. Descriptions of such terms may be found at the CATH Web site, the Structural Classification of Proteins (SCOP) Web site, and a Glaxo Wellcome tutorial on the Swiss bioinformatics Expasy Web site.[citation needed]
- Active site
- a localized combination of amino acid side groups within the tertiary (three-dimensional) or quaternary (protein subunit) structure that can interact with a chemically specific substrate and that provides the protein with biological activity. Proteins of very different amino acid sequences may fold into a structure that produces the same active site.
- Architecture
- is the relative orientations of secondary structures in a three-dimensional structure without regard to whether or not they share a similar loop structure.
- Fold (topology)
- a type of architecture that also has a conserved loop structure.
- Blocks
- is a conserved amino acid sequence pattern in a family of proteins. The pattern includes a series of possible matches at each position in the represented sequences, but there are not any inserted or deleted positions in the pattern or in the sequences. By way of contrast, sequence profiles are a type of scoring matrix that represents a similar set of patterns that includes insertions and deletions.
- Class
- a term used to classify protein domains according to their secondary structural content and organization. Four classes were originally recognized by Levitt and Chothia (1976), and several others have been added in the SCOP database. Three classes are given in the CATH database: mainly-α, mainly-β, and α–β, with the α–β class including both alternating α/β and α+β structures.
- Core
- the portion of a folded protein molecule that comprises the hydrophobic interior of α-helices and β-sheets. The compact structure brings together side groups of amino acids into close enough proximity so that they can interact. When comparing protein structures, as in the SCOP database, core is the region common to most of the structures that share a common fold or that are in the same superfamily. In structure prediction, core is sometimes defined as the arrangement of secondary structures that is likely to be conserved during evolutionary change.
- Domain (sequence context)
- a segment of a polypeptide chain that can fold into a three-dimensional structure irrespective of the presence of other segments of the chain. The separate domains of a given protein may interact extensively or may be joined only by a length of polypeptide chain. A protein with several domains may use these domains for functional interactions with different molecules.
- Family (sequence context)
- a group of proteins of similar biochemical function that are more than 50% identical when aligned. This same cutoff is still used by the Protein Information Resource (PIR). A protein family comprises proteins with the same function in different organisms (orthologous sequences) but may also include proteins in the same organism (paralogous sequences) derived from gene duplication and rearrangements. If a multiple sequence alignment of a protein family reveals a common level of similarity throughout the lengths of the proteins, PIR refers to the family as a homeomorphic family. The aligned region is referred to as a homeomorphic domain, and this region may comprise several smaller homology domains that are shared with other families. Families may be further subdivided into subfamilies or grouped into superfamilies based on respective higher or lower levels of sequence similarity. The SCOP database reports 1296 families and the CATH database (version 1.7 beta), reports 1846 families.
- When the sequences of proteins with the same function are examined in greater detail, some are found to share high sequence similarity. They are obviously members of the same family by the above criteria. However, others are found that have very little, or even insignificant, sequence similarity with other family members. In such cases, the family relationship between two distant family members A and C can often be demonstrated by finding an additional family member B that shares significant similarity with both A and C. Thus, B provides a connecting link between A and C. Another approach is to examine distant alignments for highly conserved matches.
- At a level of identity of 50%, proteins are likely to have the same three-dimensional structure, and the identical atoms in the sequence alignment will also superimpose within approximately 1 Å in the structural model. Thus, if the structure of one member of a family is known, a reliable prediction may be made for a second member of the family, and the higher the identity level, the more reliable the prediction. Protein structural modeling can be performed by examining how well the amino acid substitutions fit into the core of the three-dimensional structure.
- Family (structural context)
- as used in the FSSP database (Families of structurally similar proteins) and the DALI/FSSP Web site, two structures that have a significant level of structural similarity but not necessarily significant sequence similarity.
- Fold
- similar to structural motif, includes a larger combination of secondary structural units in the same configuration. Thus, proteins sharing the same fold have the same combination of secondary structures that are connected by similar loops. An example is the Rossman fold comprising several alternating α helices and parallel β strands. In the SCOP, CATH, and FSSP databases, the known protein structures have been classified into hierarchical levels of structural complexity with the fold as a basic level of classification.
- Homologous domain (sequence context)
- an extended sequence pattern, generally found by sequence alignment methods, that indicates a common evolutionary origin among the aligned sequences. A homology domain is generally longer than motifs. The domain may include all of a given protein sequence or only a portion of the sequence. Some domains are complex and made up of several smaller homology domains that became joined to form a larger one during evolution. A domain that covers an entire sequence is called the homeomorphic domain by PIR (Protein Information Resource).
- Module
- a region of conserved amino acid patterns comprising one or more motifs and considered to be a fundamental unit of structure or function. The presence of a module has also been used to classify proteins into families.
- Motif (sequence context)
- a conserved pattern of amino acids that is found in two or more proteins. In the Prosite catalog, a motif is an amino acid pattern that is found in a group of proteins that have a similar biochemical activity, and that often is near the active site of the protein. Examples of sequence motif databases are the Prosite catalog and the Stanford Motifs Database.[4]
- Motif (structural context)
- a combination of several secondary structural elements produced by the folding of adjacent sections of the polypeptide chain into a specific three-dimensional configuration. An example is the helix-loop-helix motif. Structural motifs are also referred to as supersecondary structures and folds.
- Position-specific scoring matrix (sequence context, also known as weight or scoring matrix)
- represents a conserved region in a multiple sequence alignment with no gaps. Each matrix column represents the variation found in one column of the multiple sequence alignment.
- Position-specific scoring matrix—3D (structural context)
- represents the amino acid variation found in an alignment of proteins that fall into the same structural class. Matrix columns represent the amino acid variation found at one amino acid position in the aligned structures.
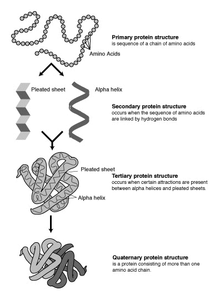
- Primary structure
- the linear amino acid sequence of a protein, which chemically is a polypeptide chain composed of amino acids joined by peptide bonds.
- Profile (sequence context)
- a scoring matrix that represents a multiple sequence alignment of a protein family. The profile is usually obtained from a well-conserved region in a multiple sequence alignment. The profile is in the form of a matrix with each column representing a position in the alignment and each row one of the amino acids. Matrix values give the likelihood of each amino acid at the corresponding position in the alignment. The profile is moved along the target sequence to locate the best scoring regions by a dynamic programming algorithm. Gaps are allowed during matching and a gap penalty is included in this case as a negative score when no amino acid is matched. A sequence profile may also be represented by a hidden Markov model, referred to as a profile HMM.
- Profile (structural context)
- a scoring matrix that represents which amino acids should fit well and which should fit poorly at sequential positions in a known protein structure. Profile columns represent sequential positions in the structure, and profile rows represent the 20 amino acids. As with a sequence profile, the structural profile is moved along a target sequence to find the highest possible alignment score by a dynamic programming algorithm. Gaps may be included and receive a penalty. The resulting score provides an indication as to whether or not the target protein might adopt such a structure.
- Quaternary structure
- the three-dimensional configuration of a protein molecule comprising several independent polypeptide chains.
- Secondary structure
- the interactions that occur between the C, O, and NH groups on amino acids in a polypeptide chain to form α-helices, β-sheets, turns, loops, and other forms, and that facilitate the folding into a three-dimensional structure.
- Superfamily
- a group of protein families of the same or different lengths that are related by distant yet detectable sequence similarity. Members of a given superfamily thus have a common evolutionary origin. Originally, Dayhoff defined the cutoff for superfamily status as being the chance that the sequences are not related of 10 6, on the basis of an alignment score (Dayhoff et al. 1978). Proteins with few identities in an alignment of the sequences but with a convincingly common number of structural and functional features are placed in the same superfamily. At the level of three-dimensional structure, superfamily proteins will share common structural features such as a common fold, but there may also be differences in the number and arrangement of secondary structures. The PIR resource uses the term homeomorphic superfamilies to refer to superfamilies that are composed of sequences that can be aligned from end to end, representing a sharing of single sequence homology domain, a region of similarity that extends throughout the alignment. This domain may also comprise smaller homology domains that are shared with other protein families and superfamilies. Although a given protein sequence may contain domains found in several superfamilies, thus indicating a complex evolutionary history, sequences will be assigned to only one homeomorphic superfamily based on the presence of similarity throughout a multiple sequence alignment. The superfamily alignment may also include regions that do not align either within or at the ends of the alignment. In contrast, sequences in the same family align well throughout the alignment.
- Supersecondary structure
- a term with similar meaning to a structural motif. Tertiary structure is the three-dimensional or globular structure formed by the packing together or folding of secondary structures of a polypeptide chain.[2]
Secondary structure
editSecondary structure prediction is a set of techniques in bioinformatics that aim to predict the local secondary structures of proteins based only on knowledge of their amino acid sequence. For proteins, a prediction consists of assigning regions of the amino acid sequence as likely alpha helices, beta strands (often termed extended conformations), or turns. The success of a prediction is determined by comparing it to the results of the DSSP algorithm (or similar e.g. STRIDE) applied to the crystal structure of the protein. Specialized algorithms have been developed for the detection of specific well-defined patterns such as transmembrane helices and coiled coils in proteins.[2]
The best modern methods of secondary structure prediction in proteins were claimed to reach 80% accuracy after using machine learning and sequence alignments;[5] this high accuracy allows the use of the predictions as feature improving fold recognition and ab initio protein structure prediction, classification of structural motifs, and refinement of sequence alignments. The accuracy of current protein secondary structure prediction methods is assessed in weekly benchmarks such as LiveBench and EVA.
Background
editEarly methods of secondary structure prediction, introduced in the 1960s and early 1970s,[6][7][8][9][10] focused on identifying likely alpha helices and were based mainly on helix-coil transition models.[11] Significantly more accurate predictions that included beta sheets were introduced in the 1970s and relied on statistical assessments based on probability parameters derived from known solved structures. These methods, applied to a single sequence, are typically at most about 60–65% accurate, and often underpredict beta sheets.[2] Since the 1980s, artificial neural networks have been applied to the prediction of protein structures.[12][13] The evolutionary conservation of secondary structures can be exploited by simultaneously assessing many homologous sequences in a multiple sequence alignment, by calculating the net secondary structure propensity of an aligned column of amino acids. In concert with larger databases of known protein structures and modern machine learning methods such as neural nets and support vector machines, these methods can achieve up to 80% overall accuracy in globular proteins.[14] The theoretical upper limit of accuracy is around 90%,[14] partly due to idiosyncrasies in DSSP assignment near the ends of secondary structures, where local conformations vary under native conditions but may be forced to assume a single conformation in crystals due to packing constraints. Moreover, the typical secondary structure prediction methods do not account for the influence of tertiary structure on formation of secondary structure; for example, a sequence predicted as a likely helix may still be able to adopt a beta-strand conformation if it is located within a beta-sheet region of the protein and its side chains pack well with their neighbors. Dramatic conformational changes related to the protein's function or environment can also alter local secondary structure.
Historical perspective
editTo date, over 20 different secondary structure prediction methods have been developed. One of the first algorithms was Chou–Fasman method, which relies predominantly on probability parameters determined from relative frequencies of each amino acid's appearance in each type of secondary structure.[15] The original Chou-Fasman parameters, determined from the small sample of structures solved in the mid-1970s, produce poor results compared to modern methods, though the parameterization has been updated since it was first published. The Chou-Fasman method is roughly 50–60% accurate in predicting secondary structures.[2]
The next notable program was the GOR method is an information theory-based method. It uses the more powerful probabilistic technique of Bayesian inference.[16] The GOR method takes into account not only the probability of each amino acid having a particular secondary structure, but also the conditional probability of the amino acid assuming each structure given the contributions of its neighbors (it does not assume that the neighbors have that same structure). The approach is both more sensitive and more accurate than that of Chou and Fasman because amino acid structural propensities are only strong for a small number of amino acids such as proline and glycine. Weak contributions from each of many neighbors can add up to strong effects overall. The original GOR method was roughly 65% accurate and is dramatically more successful in predicting alpha helices than beta sheets, which it frequently mispredicted as loops or disorganized regions.[2]
Another big step forward, was using machine learning methods. First artificial neural networks methods were used. As a training sets they use solved structures to identify common sequence motifs associated with particular arrangements of secondary structures. These methods are over 70% accurate in their predictions, although beta strands are still often underpredicted due to the lack of three-dimensional structural information that would allow assessment of hydrogen bonding patterns that can promote formation of the extended conformation required for the presence of a complete beta sheet.[2] PSIPRED and JPRED are some of the most known programs based on neural networks for protein secondary structure prediction. Next, support vector machines have proven particularly useful for predicting the locations of turns, which are difficult to identify with statistical methods.[17][18]
Extensions of machine learning techniques attempt to predict more fine-grained local properties of proteins, such as backbone dihedral angles in unassigned regions. Both SVMs[19] and neural networks[20] have been applied to this problem.[17] More recently, real-value torsion angles can be accurately predicted by SPINE-X and successfully employed for ab initio structure prediction.[21]
Other improvements
editIt is reported that in addition to the protein sequence, secondary structure formation depends on other factors. For example, it is reported that secondary structure tendencies depend also on local environment,[22] solvent accessibility of residues,[23] protein structural class,[24] and even the organism from which the proteins are obtained.[25] Based on such observations, some studies have shown that secondary structure prediction can be improved by addition of information about protein structural class,[26] residue accessible surface area[27][28] and also contact number information.[29]
Tertiary structure
editThe practical role of protein structure prediction is now more important than ever.[30] Massive amounts of protein sequence data are produced by modern large-scale DNA sequencing efforts such as the Human Genome Project. Despite community-wide efforts in structural genomics, the output of experimentally determined protein structures—typically by time-consuming and relatively expensive X-ray crystallography or NMR spectroscopy—is lagging far behind the output of protein sequences.
The protein structure prediction remains an extremely difficult and unresolved undertaking. The two main problems are the calculation of protein free energy and finding the global minimum of this energy. A protein structure prediction method must explore the space of possible protein structures which is astronomically large. These problems can be partially bypassed in "comparative" or homology modeling and fold recognition methods, in which the search space is pruned by the assumption that the protein in question adopts a structure that is close to the experimentally determined structure of another homologous protein. In contrast, the de novo protein structure prediction methods must explicitly resolve these problems. The progress and challenges in protein structure prediction have been reviewed by Zhang.[31]
Before modelling
editMost tertiary structure modelling methods, such as Rosetta, are optimized for modelling the tertiary structure of single protein domains. A step called domain parsing, or domain boundary prediction, is usually done first to split a protein into potential structural domains. As with the rest of tertiary structure prediction, this can be done comparatively from known structures[32] or ab initio with the sequence only (usually by machine learning, assisted by covariation).[33] The structures for individual domains are docked together in a process called domain assembly to form the final tertiary structure.[34][35]
Ab initio protein modelling
editEnergy- and fragment-based methods
editAb initio- or de novo- protein modelling methods seek to build three-dimensional protein models "from scratch", i.e., based on physical principles rather than (directly) on previously solved structures. There are many possible procedures that either attempt to mimic protein folding or apply some stochastic method to search possible solutions (i.e., global optimization of a suitable energy function). These procedures tend to require vast computational resources, and have thus only been carried out for tiny proteins. To predict protein structure de novo for larger proteins will require better algorithms and larger computational resources like those afforded by either powerful supercomputers (such as Blue Gene or MDGRAPE-3) or distributed computing (such as Folding@home, the Human Proteome Folding Project and Rosetta@Home). Although these computational barriers are vast, the potential benefits of structural genomics (by predicted or experimental methods) make ab initio structure prediction an active research field.[31]
As of 2009, a 50-residue protein could be simulated atom-by-atom on a supercomputer for 1 millisecond.[36] As of 2012, comparable stable-state sampling could be done on a standard desktop with a new graphics card and more sophisticated algorithms.[37] A much larger simulation timescales can be achieved using coarse-grained modeling.[38][39]
Evolutionary covariation to predict 3D contacts
editAs sequencing became more commonplace in the 1990s several groups used protein sequence alignments to predict correlated mutations and it was hoped that these coevolved residues could be used to predict tertiary structure (using the analogy to distance constraints from experimental procedures such as NMR). The assumption is when single residue mutations are slightly deleterious, compensatory mutations may occur to restabilize residue-residue interactions. This early work used what are known as local methods to calculate correlated mutations from protein sequences, but suffered from indirect false correlations which result from treating each pair of residues as independent of all other pairs.[40][41][42]
In 2011, a different, and this time global statistical approach, demonstrated that predicted coevolved residues were sufficient to predict the 3D fold of a protein, providing there are enough sequences available (>1,000 homologous sequences are needed).[43] The method, EVfold, uses no homology modeling, threading or 3D structure fragments and can be run on a standard personal computer even for proteins with hundreds of residues. The accuracy of the contacts predicted using this and related approaches has now been demonstrated on many known structures and contact maps,[44][45][46] including the prediction of experimentally unsolved transmembrane proteins.[47]
Comparative protein modeling
editComparative protein modeling uses previously solved structures as starting points, or templates. This is effective because it appears that although the number of actual proteins is vast, there is a limited set of tertiary structural motifs to which most proteins belong. It has been suggested that there are only around 2,000 distinct protein folds in nature, though there are many millions of different proteins. The comparative protein modeling can combine with the evolutionary covariation in the structure prediction.[48]
These methods may also be split into two groups:[31]
- Homology modeling is based on the reasonable assumption that two homologous proteins will share very similar structures. Because a protein's fold is more evolutionarily conserved than its amino acid sequence, a target sequence can be modeled with reasonable accuracy on a very distantly related template, provided that the relationship between target and template can be discerned through sequence alignment. It has been suggested that the primary bottleneck in comparative modelling arises from difficulties in alignment rather than from errors in structure prediction given a known-good alignment.[49] Unsurprisingly, homology modelling is most accurate when the target and template have similar sequences.
- Protein threading[50] scans the amino acid sequence of an unknown structure against a database of solved structures. In each case, a scoring function is used to assess the compatibility of the sequence to the structure, thus yielding possible three-dimensional models. This type of method is also known as 3D-1D fold recognition due to its compatibility analysis between three-dimensional structures and linear protein sequences. This method has also given rise to methods performing an inverse folding search by evaluating the compatibility of a given structure with a large database of sequences, thus predicting which sequences have the potential to produce a given fold.
Modeling of side-chain conformations
editAccurate packing of the amino acid side chains represents a separate problem in protein structure prediction. Methods that specifically address the problem of predicting side-chain geometry include dead-end elimination and the self-consistent mean field methods. The side chain conformations with low energy are usually determined on the rigid polypeptide backbone and using a set of discrete side chain conformations known as "rotamers." The methods attempt to identify the set of rotamers that minimize the model's overall energy.
These methods use rotamer libraries, which are collections of favorable conformations for each residue type in proteins. Rotamer libraries may contain information about the conformation, its frequency, and the standard deviations about mean dihedral angles, which can be used in sampling.[51] Rotamer libraries are derived from structural bioinformatics or other statistical analysis of side-chain conformations in known experimental structures of proteins, such as by clustering the observed conformations for tetrahedral carbons near the staggered (60°, 180°, −60°) values.
Rotamer libraries can be backbone-independent, secondary-structure-dependent, or backbone-dependent. Backbone-independent rotamer libraries make no reference to backbone conformation, and are calculated from all available side chains of a certain type (for instance, the first example of a rotamer library, done by Ponder and Richards at Yale in 1987).[52] Secondary-structure-dependent libraries present different dihedral angles and/or rotamer frequencies for -helix, -sheet, or coil secondary structures.[53] Backbone-dependent rotamer libraries present conformations and/or frequencies dependent on the local backbone conformation as defined by the backbone dihedral angles and , regardless of secondary structure.[54]
The modern versions of these libraries as used in most software are presented as multidimensional distributions of probability or frequency, where the peaks correspond to the dihedral-angle conformations considered as individual rotamers in the lists. Some versions are based on very carefully curated data and are used primarily for structure validation,[55] while others emphasize relative frequencies in much larger data sets and are the form used primarily for structure prediction, such as the Dunbrack rotamer libraries.[56]
Side-chain packing methods are most useful for analyzing the protein's hydrophobic core, where side chains are more closely packed; they have more difficulty addressing the looser constraints and higher flexibility of surface residues, which often occupy multiple rotamer conformations rather than just one.[57][58]
Quaternary structure
editIn the case of complexes of two or more proteins, where the structures of the proteins are known or can be predicted with high accuracy, protein–protein docking methods can be used to predict the structure of the complex. Information of the effect of mutations at specific sites on the affinity of the complex helps to understand the complex structure and to guide docking methods.
Software
editA great number of software tools for protein structure prediction exist. Approaches include homology modeling, protein threading, ab initio methods, secondary structure prediction, and transmembrane helix and signal peptide prediction. In particular, deep learning based on long short-term memory has been used for this purpose since 2007, when it was successfully applied to protein homology detection[59] and to predict subcellular localization of proteins.[60] Some recent successful methods based on the CASP experiments include I-TASSER, HHpred and AlphaFold. In 2021, AlphaFold was reported to perform best.[61]
Knowing the structure of a protein often allows functional prediction as well. For instance, collagen is folded into a long-extended fiber-like chain and it makes it a fibrous protein. Recently, several techniques have been developed to predict protein folding and thus protein structure, for example, Itasser, and AlphaFold.
AI methods
editAlphaFold was one of the first AIs to predict protein structures. It was introduced by Google's DeepMind in the 13th CASP competition, which was held in 2018.[61] AlphaFold relies on a neural network approach, which directly predicts the 3D coordinates of all non-hydrogen atoms for a given protein using the amino acid sequence and aligned homologous sequences. The AlphaFold network consists of a trunk which processes the inputs through repeated layers, and a structure module which introduces an explicit 3D structure.[61] Earlier neural networks for protein structure prediction used LSTM.[59][60]
Since AlphaFold outputs protein coordinates directly, AlphaFold produces predictions in graphics processing unit (GPU) minutes to GPU hours, depending on the length of protein sequence.[61]
Current AI methods and databases of predicted protein structures
editAlphaFold2, was introduced in CASP14, and is capable of predicting protein structures to near experimental accuracy.[62] AlphaFold was swiftly followed by RoseTTAFold[63] and later by OmegaFold and the ESM Metagenomic Atlas.[64] In a recent study, Sommer et al. 2022 demonstrated the application of protein structure prediction in genome annotation, specifically in identifying functional protein isoforms using computationally predicted structures, available at https://www.isoform.io.[65] This study highlights the promise of protein structure prediction as a genome annotation tool and presents a practical, structure-guided approach that can be used to enhance the annotation of any genome.
The European Bioinformatics Institute together with DeepMind have constructed the AlphaFold – EBI database[66] for predicted protein structures.[67]
Evaluation of automatic structure prediction servers
editCASP, which stands for Critical Assessment of Techniques for Protein Structure Prediction, is a community-wide experiment for protein structure prediction taking place every two years since 1994. CASP provides with an opportunity to assess the quality of available human, non-automated methodology (human category) and automatic servers for protein structure prediction (server category, introduced in the CASP7).[68]
The CAMEO3D Continuous Automated Model EvaluatiOn Server evaluates automated protein structure prediction servers on a weekly basis using blind predictions for newly release protein structures. CAMEO publishes the results on its website.
See also
edit- Protein design
- Protein function prediction
- Protein–protein interaction prediction
- Gene prediction
- Protein structure prediction software
- De novo protein structure prediction
- Molecular design software
- Molecular modeling software
- Modelling biological systems
- Fragment libraries
- Lattice proteins
- Statistical potential
- Structure atlas of human genome
- Protein circular dichroism data bank
References
edit- ^ Iupac-Iub Comm. On Biochem. Nomenclature (1 September 1970). "IUPAC-IUB Commission on Biochemical Nomenclature. Abbreviations and symbols for the description of the conformation of polypeptide chains. Tentative rules (1969)". Biochemistry. 9 (18): 3471–3479. doi:10.1021/bi00820a001. PMID 5509841. S2CID 196933.
- ^ a b c d e f g h Mount DM (2004). Bioinformatics: Sequence and Genome Analysis. Vol. 2. Cold Spring Harbor Laboratory Press. ISBN 978-0-87969-712-9.
- ^ Yousif, Ragheed Hussam, et al. "Exploring the Molecular Interactions between Neoculin and the Human Sweet Taste Receptors through Computational Approaches." Sains Malaysiana 49.3 (2020): 517-525.
- ^ Huang JY, Brutlag DL (January 2001). "The EMOTIF database". Nucleic Acids Research. 29 (1): 202–4. doi:10.1093/nar/29.1.202. PMC 29837. PMID 11125091.
- ^ Pirovano W, Heringa J (2010). "Protein Secondary Structure Prediction". Data Mining Techniques for the Life Sciences. Methods in Molecular Biology. Vol. 609. pp. 327–48. doi:10.1007/978-1-60327-241-4_19. ISBN 978-1-60327-240-7. PMID 20221928.
- ^ Guzzo AV (November 1965). "The influence of amino-acid sequence on protein structure". Biophysical Journal. 5 (6): 809–22. Bibcode:1965BpJ.....5..809G. doi:10.1016/S0006-3495(65)86753-4. PMC 1367904. PMID 5884309.
- ^ Prothero JW (May 1966). "Correlation between the distribution of amino acids and alpha helices". Biophysical Journal. 6 (3): 367–70. Bibcode:1966BpJ.....6..367P. doi:10.1016/S0006-3495(66)86662-6. PMC 1367951. PMID 5962284.
- ^ Schiffer M, Edmundson AB (March 1967). "Use of helical wheels to represent the structures of proteins and to identify segments with helical potential". Biophysical Journal. 7 (2): 121–35. Bibcode:1967BpJ.....7..121S. doi:10.1016/S0006-3495(67)86579-2. PMC 1368002. PMID 6048867.
- ^ Kotelchuck D, Scheraga HA (January 1969). "The influence of short-range interactions on protein onformation. II. A model for predicting the alpha-helical regions of proteins". Proceedings of the National Academy of Sciences of the United States of America. 62 (1): 14–21. Bibcode:1969PNAS...62...14K. doi:10.1073/pnas.62.1.14. PMC 285948. PMID 5253650.
- ^ Lewis PN, Go N, Go M, Kotelchuck D, Scheraga HA (April 1970). "Helix probability profiles of denatured proteins and their correlation with native structures". Proceedings of the National Academy of Sciences of the United States of America. 65 (4): 810–5. Bibcode:1970PNAS...65..810L. doi:10.1073/pnas.65.4.810. PMC 282987. PMID 5266152.
- ^ Froimowitz M, Fasman GD (1974). "Prediction of the secondary structure of proteins using the helix-coil transition theory". Macromolecules. 7 (5): 583–9. Bibcode:1974MaMol...7..583F. doi:10.1021/ma60041a009. PMID 4371089.
- ^ Qian, Ning; Sejnowski, Terry J. (1988). "Predicting the secondary structure of globular proteins using neural network models" (PDF). Journal of Molecular Biology. 202 (4): 865–884. doi:10.1016/0022-2836(88)90564-5. PMID 3172241. Qian1988.
- ^ Rost, Burkhard; Sander, Chris (1993). "Prediction of protein secondary structure at better than 70% accuracy" (PDF). Journal of Molecular Biology. 232 (2): 584–599. doi:10.1006/jmbi.1993.1413. PMID 8345525. Rost1993. Archived from the original (PDF) on 2019-01-31. Retrieved 2023-04-20.
- ^ a b Dor O, Zhou Y (March 2007). "Achieving 80% ten-fold cross-validated accuracy for secondary structure prediction by large-scale training". Proteins. 66 (4): 838–45. doi:10.1002/prot.21298. PMID 17177203. S2CID 14759081.
- ^ Chou PY, Fasman GD (January 1974). "Prediction of protein conformation". Biochemistry. 13 (2): 222–45. doi:10.1021/bi00699a002. PMID 4358940.
- ^ Garnier J, Osguthorpe DJ, Robson B (March 1978). "Analysis of the accuracy and implications of simple methods for predicting the secondary structure of globular proteins". Journal of Molecular Biology. 120 (1): 97–120. doi:10.1016/0022-2836(78)90297-8. PMID 642007.
- ^ a b Pham TH, Satou K, Ho TB (April 2005). "Support vector machines for prediction and analysis of beta and gamma-turns in proteins". Journal of Bioinformatics and Computational Biology. 3 (2): 343–58. doi:10.1142/S0219720005001089. PMID 15852509.
- ^ Zhang Q, Yoon S, Welsh WJ (May 2005). "Improved method for predicting beta-turn using support vector machine". Bioinformatics. 21 (10): 2370–4. doi:10.1093/bioinformatics/bti358. PMID 15797917.
- ^ Zimmermann O, Hansmann UH (December 2006). "Support vector machines for prediction of dihedral angle regions". Bioinformatics. 22 (24): 3009–15. doi:10.1093/bioinformatics/btl489. PMID 17005536.
- ^ Kuang R, Leslie CS, Yang AS (July 2004). "Protein backbone angle prediction with machine learning approaches". Bioinformatics. 20 (10): 1612–21. doi:10.1093/bioinformatics/bth136. PMID 14988121.
- ^ Faraggi E, Yang Y, Zhang S, Zhou Y (November 2009). "Predicting continuous local structure and the effect of its substitution for secondary structure in fragment-free protein structure prediction". Structure. 17 (11): 1515–27. doi:10.1016/j.str.2009.09.006. PMC 2778607. PMID 19913486.
- ^ Zhong L, Johnson WC (May 1992). "Environment affects amino acid preference for secondary structure". Proceedings of the National Academy of Sciences of the United States of America. 89 (10): 4462–5. Bibcode:1992PNAS...89.4462Z. doi:10.1073/pnas.89.10.4462. PMC 49102. PMID 1584778.
- ^ Macdonald JR, Johnson WC (June 2001). "Environmental features are important in determining protein secondary structure". Protein Science. 10 (6): 1172–7. doi:10.1110/ps.420101. PMC 2374018. PMID 11369855.
- ^ Costantini S, Colonna G, Facchiano AM (April 2006). "Amino acid propensities for secondary structures are influenced by the protein structural class". Biochemical and Biophysical Research Communications. 342 (2): 441–51. doi:10.1016/j.bbrc.2006.01.159. PMID 16487481.
- ^ Marashi SA, Behrouzi R, Pezeshk H (January 2007). "Adaptation of proteins to different environments: a comparison of proteome structural properties in Bacillus subtilis and Escherichia coli". Journal of Theoretical Biology. 244 (1): 127–32. Bibcode:2007JThBi.244..127M. doi:10.1016/j.jtbi.2006.07.021. PMID 16945389.
- ^ Costantini S, Colonna G, Facchiano AM (October 2007). "PreSSAPro: a software for the prediction of secondary structure by amino acid properties". Computational Biology and Chemistry. 31 (5–6): 389–92. doi:10.1016/j.compbiolchem.2007.08.010. PMID 17888742.
- ^ Momen-Roknabadi A, Sadeghi M, Pezeshk H, Marashi SA (August 2008). "Impact of residue accessible surface area on the prediction of protein secondary structures". BMC Bioinformatics. 9: 357. doi:10.1186/1471-2105-9-357. PMC 2553345. PMID 18759992.
- ^ Adamczak R, Porollo A, Meller J (May 2005). "Combining prediction of secondary structure and solvent accessibility in proteins". Proteins. 59 (3): 467–75. doi:10.1002/prot.20441. PMID 15768403. S2CID 13267624.
- ^ Lakizadeh A, Marashi SA (2009). "Addition of contact number information can improve protein secondary structure prediction by neural networks" (PDF). Excli J. 8: 66–73.
- ^ Dorn, Márcio; e Silva, Mariel Barbachan; Buriol, Luciana S.; Lamb, Luis C. (2014-12-01). "Three-dimensional protein structure prediction: Methods and computational strategies". Computational Biology and Chemistry. 53: 251–276. doi:10.1016/j.compbiolchem.2014.10.001. ISSN 1476-9271. PMID 25462334.
- ^ a b c Zhang Y (June 2008). "Progress and challenges in protein structure prediction". Current Opinion in Structural Biology. 18 (3): 342–8. doi:10.1016/j.sbi.2008.02.004. PMC 2680823. PMID 18436442.
- ^ Ovchinnikov S, Kim DE, Wang RY, Liu Y, DiMaio F, Baker D (September 2016). "Improved de novo structure prediction in CASP11 by incorporating coevolution information into Rosetta". Proteins. 84 (Suppl 1): 67–75. doi:10.1002/prot.24974. PMC 5490371. PMID 26677056.
- ^ Hong SH, Joo K, Lee J (November 2018). "ConDo: Protein domain boundary prediction using coevolutionary information". Bioinformatics. 35 (14): 2411–2417. doi:10.1093/bioinformatics/bty973. PMID 30500873.
- ^ Wollacott AM, Zanghellini A, Murphy P, Baker D (February 2007). "Prediction of structures of multidomain proteins from structures of the individual domains". Protein Science. 16 (2): 165–75. doi:10.1110/ps.062270707. PMC 2203296. PMID 17189483.
- ^ Xu D, Jaroszewski L, Li Z, Godzik A (July 2015). "AIDA: ab initio domain assembly for automated multi-domain protein structure prediction and domain-domain interaction prediction". Bioinformatics. 31 (13): 2098–105. doi:10.1093/bioinformatics/btv092. PMC 4481839. PMID 25701568.
- ^ Shaw DE, Dror RO, Salmon JK, Grossman JP, Mackenzie KM, Bank JA, Young C, Deneroff MM, Batson B, Bowers KJ, Chow E (2009). Millisecond-scale molecular dynamics simulations on Anton. Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis – SC '09. p. 1. doi:10.1145/1654059.1654126. ISBN 9781605587448.
- ^ Pierce LC, Salomon-Ferrer R, de Oliveira CA, McCammon JA, Walker RC (September 2012). "Routine Access to Millisecond Time Scale Events with Accelerated Molecular Dynamics". Journal of Chemical Theory and Computation. 8 (9): 2997–3002. doi:10.1021/ct300284c. PMC 3438784. PMID 22984356.
- ^ Kmiecik S, Gront D, Kolinski M, Wieteska L, Dawid AE, Kolinski A (July 2016). "Coarse-Grained Protein Models and Their Applications". Chemical Reviews. 116 (14): 7898–936. doi:10.1021/acs.chemrev.6b00163. PMID 27333362.
- ^ Cheung NJ, Yu W (November 2018). "De novo protein structure prediction using ultra-fast molecular dynamics simulation". PLOS ONE. 13 (11): e0205819. Bibcode:2018PLoSO..1305819C. doi:10.1371/journal.pone.0205819. PMC 6245515. PMID 30458007.
- ^ Göbel U, Sander C, Schneider R, Valencia A (April 1994). "Correlated mutations and residue contacts in proteins". Proteins. 18 (4): 309–17. doi:10.1002/prot.340180402. PMID 8208723. S2CID 14978727.
- ^ Taylor WR, Hatrick K (March 1994). "Compensating changes in protein multiple sequence alignments". Protein Engineering. 7 (3): 341–8. doi:10.1093/protein/7.3.341. PMID 8177883.
- ^ Neher E (January 1994). "How frequent are correlated changes in families of protein sequences?". Proceedings of the National Academy of Sciences of the United States of America. 91 (1): 98–102. Bibcode:1994PNAS...91...98N. doi:10.1073/pnas.91.1.98. PMC 42893. PMID 8278414.
- ^ Marks DS, Colwell LJ, Sheridan R, Hopf TA, Pagnani A, Zecchina R, Sander C (2011). "Protein 3D structure computed from evolutionary sequence variation". PLOS ONE. 6 (12): e28766. Bibcode:2011PLoSO...628766M. doi:10.1371/journal.pone.0028766. PMC 3233603. PMID 22163331.
- ^ Burger L, van Nimwegen E (January 2010). "Disentangling direct from indirect co-evolution of residues in protein alignments". PLOS Computational Biology. 6 (1): e1000633. Bibcode:2010PLSCB...6E0633B. doi:10.1371/journal.pcbi.1000633. PMC 2793430. PMID 20052271.
- ^ Morcos F, Pagnani A, Lunt B, Bertolino A, Marks DS, Sander C, Zecchina R, Onuchic JN, Hwa T, Weigt M (December 2011). "Direct-coupling analysis of residue coevolution captures native contacts across many protein families". Proceedings of the National Academy of Sciences of the United States of America. 108 (49): E1293-301. arXiv:1110.5223. Bibcode:2011PNAS..108E1293M. doi:10.1073/pnas.1111471108. PMC 3241805. PMID 22106262.
- ^ Nugent T, Jones DT (June 2012). "Accurate de novo structure prediction of large transmembrane protein domains using fragment-assembly and correlated mutation analysis". Proceedings of the National Academy of Sciences of the United States of America. 109 (24): E1540-7. Bibcode:2012PNAS..109E1540N. doi:10.1073/pnas.1120036109. PMC 3386101. PMID 22645369.
- ^ Hopf TA, Colwell LJ, Sheridan R, Rost B, Sander C, Marks DS (June 2012). "Three-dimensional structures of membrane proteins from genomic sequencing". Cell. 149 (7): 1607–21. doi:10.1016/j.cell.2012.04.012. PMC 3641781. PMID 22579045.
- ^ Jin, Shikai; Chen, Mingchen; Chen, Xun; Bueno, Carlos; Lu, Wei; Schafer, Nicholas P.; Lin, Xingcheng; Onuchic, José N.; Wolynes, Peter G. (9 June 2020). "Protein Structure Prediction in CASP13 Using AWSEM-Suite". Journal of Chemical Theory and Computation. 16 (6): 3977–3988. doi:10.1021/acs.jctc.0c00188. PMID 32396727. S2CID 218618842.
- ^ Zhang Y, Skolnick J (January 2005). "The protein structure prediction problem could be solved using the current PDB library". Proceedings of the National Academy of Sciences of the United States of America. 102 (4): 1029–34. Bibcode:2005PNAS..102.1029Z. doi:10.1073/pnas.0407152101. PMC 545829. PMID 15653774.
- ^ Bowie JU, Lüthy R, Eisenberg D (July 1991). "A method to identify protein sequences that fold into a known three-dimensional structure". Science. 253 (5016): 164–70. Bibcode:1991Sci...253..164B. doi:10.1126/science.1853201. PMID 1853201.
- ^ Dunbrack RL (August 2002). "Rotamer libraries in the 21st century". Current Opinion in Structural Biology. 12 (4): 431–40. doi:10.1016/S0959-440X(02)00344-5. PMID 12163064.
- ^ Ponder JW, Richards FM (February 1987). "Tertiary templates for proteins. Use of packing criteria in the enumeration of allowed sequences for different structural classes". Journal of Molecular Biology. 193 (4): 775–91. doi:10.1016/0022-2836(87)90358-5. PMID 2441069.
- ^ Lovell SC, Word JM, Richardson JS, Richardson DC (August 2000). "The penultimate rotamer library". Proteins. 40 (3): 389–408. doi:10.1002/1097-0134(20000815)40:3<389::AID-PROT50>3.0.CO;2-2. PMID 10861930. S2CID 3055173.
- ^ Shapovalov MV, Dunbrack RL (June 2011). "A smoothed backbone-dependent rotamer library for proteins derived from adaptive kernel density estimates and regressions". Structure. 19 (6): 844–58. doi:10.1016/j.str.2011.03.019. PMC 3118414. PMID 21645855.
- ^ Chen VB, Arendall WB, Headd JJ, Keedy DA, Immormino RM, Kapral GJ, Murray LW, Richardson JS, Richardson DC (January 2010). "MolProbity: all-atom structure validation for macromolecular crystallography". Acta Crystallographica. Section D, Biological Crystallography. 66 (Pt 1): 12–21. Bibcode:2010AcCrD..66...12C. doi:10.1107/S0907444909042073. PMC 2803126. PMID 20057044.
- ^ Bower MJ, Cohen FE, Dunbrack RL (April 1997). "Prediction of protein side-chain rotamers from a backbone-dependent rotamer library: a new homology modeling tool". Journal of Molecular Biology. 267 (5): 1268–82. doi:10.1006/jmbi.1997.0926. PMID 9150411.
- ^ Voigt CA, Gordon DB, Mayo SL (June 2000). "Trading accuracy for speed: A quantitative comparison of search algorithms in protein sequence design". Journal of Molecular Biology. 299 (3): 789–803. CiteSeerX 10.1.1.138.2023. doi:10.1006/jmbi.2000.3758. PMID 10835284.
- ^ Krivov GG, Shapovalov MV, Dunbrack RL (December 2009). "Improved prediction of protein side-chain conformations with SCWRL4". Proteins. 77 (4): 778–95. doi:10.1002/prot.22488. PMC 2885146. PMID 19603484.
- ^ a b Hochreiter, S.; Heusel, M.; Obermayer, K. (2007). "Fast model-based protein homology detection without alignment". Bioinformatics. 23 (14): 1728–1736. doi:10.1093/bioinformatics/btm247. PMID 17488755.
- ^ a b Thireou, T.; Reczko, M. (2007). "Bidirectional Long Short-Term Memory Networks for predicting the subcellular localization of eukaryotic proteins". IEEE/ACM Transactions on Computational Biology and Bioinformatics. 4 (3): 441–446. doi:10.1109/tcbb.2007.1015. PMID 17666763. S2CID 11787259.
- ^ a b c d Jumper, John; Evans, Richard; Pritzel, Alexander; Green, Tim; Figurnov, Michael; Ronneberger, Olaf; Tunyasuvunakool, Kathryn; Bates, Russ; Žídek, Augustin; Potapenko, Anna; Bridgland, Alex (August 2021). "Highly accurate protein structure prediction with AlphaFold". Nature. 596 (7873): 583–589. Bibcode:2021Natur.596..583J. doi:10.1038/s41586-021-03819-2. ISSN 1476-4687. PMC 8371605. PMID 34265844.
- ^ Jumper J, Evans R, Pritzel A, Green T, Figurnov M, Ronneberger O, et al. (August 2021). "Highly accurate protein structure prediction with AlphaFold". Nature. 596 (7873): 583–589. Bibcode:2021Natur.596..583J. doi:10.1038/s41586-021-03819-2. PMC 8371605. PMID 34265844.
- ^ Baek M, DiMaio F, Anishchenko I, Dauparas J, Ovchinnikov S, Lee GR, et al. (August 2021). "Accurate prediction of protein structures and interactions using a three-track neural network". Science. 373 (6557): 871–876. Bibcode:2021Sci...373..871B. doi:10.1126/science.abj8754. PMC 7612213. PMID 34282049.
- ^ Callaway E (November 2022). "AlphaFold's new rival? Meta AI predicts shape of 600 million proteins". Nature. 611 (7935): 211–212. Bibcode:2022Natur.611..211C. doi:10.1038/d41586-022-03539-1. PMID 36319775. S2CID 253257926.
- ^ Sommer, Markus J.; Cha, Sooyoung; Varabyou, Ales; Rincon, Natalia; Park, Sukhwan; Minkin, Ilia; Pertea, Mihaela; Steinegger, Martin; Salzberg, Steven L. (2022-12-15). "Structure-guided isoform identification for the human transcriptome". eLife. 11: e82556. doi:10.7554/eLife.82556. PMC 9812405. PMID 36519529.
- ^ "AlphaFold Protein Structure Database". EMBL-EBI. Retrieved November 30, 2022.
- ^ Varadi M, Anyango S, Deshpande M, Nair S, Natassia C, Yordanova G, et al. (January 2022). "AlphaFold Protein Structure Database: massively expanding the structural coverage of protein-sequence space with high-accuracy models". Nucleic Acids Res. 50 (D1): D439 – D444. doi:10.1093/nar/gkab1061. PMC 8728224. PMID 34791371.
- ^ Battey JN, Kopp J, Bordoli L, Read RJ, Clarke ND, Schwede T (2007). "Automated server predictions in CASP7". Proteins. 69 (Suppl 8): 68–82. doi:10.1002/prot.21761. PMID 17894354. S2CID 29879391.
Further reading
edit- Majorek K, Kozlowski L, Jakalski M, Bujnicki JM (December 18, 2008). "Chapter 2: First Steps of Protein Structure Prediction" (PDF). In Bujnicki J (ed.). Prediction of Protein Structures, Functions, and Interactions. John Wiley & Sons, Ltd. pp. 39–62. doi:10.1002/9780470741894.ch2. ISBN 9780470517673.[permanent dead link]
- Baker D, Sali A (October 2001). "Protein structure prediction and structural genomics". Science. 294 (5540): 93–6. Bibcode:2001Sci...294...93B. doi:10.1126/science.1065659. PMID 11588250. S2CID 7193705.
- Kelley LA, Sternberg MJ (2009). "Protein structure prediction on the Web: a case study using the Phyre server" (PDF). Nature Protocols. 4 (3): 363–71. doi:10.1038/nprot.2009.2. hdl:10044/1/18157. PMID 19247286. S2CID 12497300.
- Kryshtafovych A, Fidelis K (April 2009). "Protein structure prediction and model quality assessment". Drug Discovery Today. 14 (7–8): 386–93. doi:10.1016/j.drudis.2008.11.010. PMC 2808711. PMID 19100336.
- Qu X, Swanson R, Day R, Tsai J (June 2009). "A guide to template based structure prediction". Current Protein & Peptide Science. 10 (3): 270–85. doi:10.2174/138920309788452182. PMID 19519455.
- Daga PR, Patel RY, Doerksen RJ (2010). "Template-based protein modeling: recent methodological advances". Current Topics in Medicinal Chemistry. 10 (1): 84–94. doi:10.2174/156802610790232314. PMC 5943704. PMID 19929829.
- Fiser, A. (2010). "Template-Based Protein Structure Modeling". Computational Biology. Methods in Molecular Biology. Vol. 673. pp. 73–94. doi:10.1007/978-1-60761-842-3_6. ISBN 978-1-60761-841-6. PMC 4108304. PMID 20835794.
- Cozzetto D, Tramontano A (December 2008). "Advances and pitfalls in protein structure prediction". Current Protein & Peptide Science. 9 (6): 567–77. doi:10.2174/138920308786733958. PMID 19075747.
- Nayeem A, Sitkoff D, Krystek S (April 2006). "A comparative study of available software for high-accuracy homology modeling: from sequence alignments to structural models". Protein Science. 15 (4): 808–24. doi:10.1110/ps.051892906. PMC 2242473. PMID 16600967.
External links
edit- Official website, Protein Structure Prediction Center, CASP experiments
- ExPASy Proteomics tools – list of prediction tools and servers