In mathematics, an infinite sequence of numbers is called constant-recursive if it satisfies an equation of the form
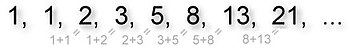
for all , where are constants. The equation is called a linear recurrence relation. The concept is also known as a linear recurrence sequence, linear-recursive sequence, linear-recurrent sequence, or a C-finite sequence.[1]
For example, the Fibonacci sequence
- ,
is constant-recursive because it satisfies the linear recurrence : each number in the sequence is the sum of the previous two.[2] Other examples include the power of two sequence , where each number is the sum of twice the previous number, and the square number sequence . All arithmetic progressions, all geometric progressions, and all polynomials are constant-recursive. However, not all sequences are constant-recursive; for example, the factorial sequence is not constant-recursive.
Constant-recursive sequences are studied in combinatorics and the theory of finite differences. They also arise in algebraic number theory, due to the relation of the sequence to polynomial roots; in the analysis of algorithms, as the running time of simple recursive functions; and in the theory of formal languages, where they count strings up to a given length in a regular language. Constant-recursive sequences are closed under important mathematical operations such as term-wise addition, term-wise multiplication, and Cauchy product.
The Skolem–Mahler–Lech theorem states that the zeros of a constant-recursive sequence have a regularly repeating (eventually periodic) form. The Skolem problem, which asks for an algorithm to determine whether a linear recurrence has at least one zero, is an unsolved problem in mathematics.
Definition
editA constant-recursive sequence is any sequence of integers, rational numbers, algebraic numbers, real numbers, or complex numbers (written as as a shorthand) satisfying a formula of the form
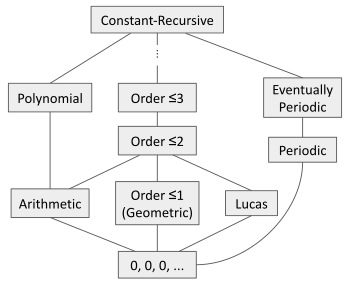
for all for some fixed coefficients ranging over the same domain as the sequence (integers, rational numbers, algebraic numbers, real numbers, or complex numbers). The equation is called a linear recurrence with constant coefficients of order d. The order of the sequence is the smallest positive integer such that the sequence satisfies a recurrence of order d, or for the everywhere-zero sequence.[citation needed]
The definition above allows eventually-periodic sequences such as and . Some authors require that , which excludes such sequences.[3][4][5]
Examples
edit| Name | Order ( ) | First few values | Recurrence (for ) | Generating function | OEIS |
|---|---|---|---|---|---|
| Zero sequence | 0 | 0, 0, 0, 0, 0, 0, ... | A000004 | ||
| One sequence | 1 | 1, 1, 1, 1, 1, 1, ... | A000012 | ||
| Characteristic function of | 1 | 1, 0, 0, 0, 0, 0, ... | A000007 | ||
| Powers of two | 1 | 1, 2, 4, 8, 16, 32, ... | A000079 | ||
| Powers of −1 | 1 | 1, −1, 1, −1, 1, −1, ... | A033999 | ||
| Characteristic function of | 2 | 0, 1, 0, 0, 0, 0, ... | A063524 | ||
| Decimal expansion of 1/6 | 2 | 1, 6, 6, 6, 6, 6, ... | A020793 | ||
| Decimal expansion of 1/11 | 2 | 0, 9, 0, 9, 0, 9, ... | A010680 | ||
| Nonnegative integers | 2 | 0, 1, 2, 3, 4, 5, ... | A001477 | ||
| Odd positive integers | 2 | 1, 3, 5, 7, 9, 11, ... | A005408 | ||
| Fibonacci numbers | 2 | 0, 1, 1, 2, 3, 5, 8, 13, ... | A000045 | ||
| Lucas numbers | 2 | 2, 1, 3, 4, 7, 11, 18, 29, ... | A000032 | ||
| Pell numbers | 2 | 0, 1, 2, 5, 12, 29, 70, ... | A000129 | ||
| Powers of two interleaved with 0s | 2 | 1, 0, 2, 0, 4, 0, 8, 0, ... | A077957 | ||
| Inverse of 6th cyclotomic polynomial | 2 | 1, 1, 0, −1, −1, 0, 1, 1, ... | A010892 | ||
| Triangular numbers | 3 | 0, 1, 3, 6, 10, 15, 21, ... | A000217 |
Fibonacci and Lucas sequences
editThe sequence 0, 1, 1, 2, 3, 5, 8, 13, ... of Fibonacci numbers is constant-recursive of order 2 because it satisfies the recurrence with . For example, and . The sequence 2, 1, 3, 4, 7, 11, ... of Lucas numbers satisfies the same recurrence as the Fibonacci sequence but with initial conditions and . More generally, every Lucas sequence is constant-recursive of order 2.[2]
Arithmetic progressions
editFor any and any , the arithmetic progression is constant-recursive of order 2, because it satisfies . Generalizing this, see polynomial sequences below.[citation needed]
Geometric progressions
editFor any and , the geometric progression is constant-recursive of order 1, because it satisfies . This includes, for example, the sequence 1, 2, 4, 8, 16, ... as well as the rational number sequence .[citation needed]
Eventually periodic sequences
editA sequence that is eventually periodic with period length is constant-recursive, since it satisfies for all , where the order is the length of the initial segment including the first repeating block. Examples of such sequences are 1, 0, 0, 0, ... (order 1) and 1, 6, 6, 6, ... (order 2).[citation needed]
Polynomial sequences
editA sequence defined by a polynomial is constant-recursive. The sequence satisfies a recurrence of order (where is the degree of the polynomial), with coefficients given by the corresponding element of the binomial transform.[7][8] The first few such equations are
- for a degree 0 (that is, constant) polynomial,
- for a degree 1 or less polynomial,
- for a degree 2 or less polynomial, and
- for a degree 3 or less polynomial.
A sequence obeying the order-d equation also obeys all higher order equations. These identities may be proved in a number of ways, including via the theory of finite differences.[9] Any sequence of integer, real, or complex values can be used as initial conditions for a constant-recursive sequence of order . If the initial conditions lie on a polynomial of degree or less, then the constant-recursive sequence also obeys a lower order equation.
Enumeration of words in a regular language
editLet be a regular language, and let be the number of words of length in . Then is constant-recursive.[10] For example, for the language of all binary strings, for the language of all unary strings, and for the language of all binary strings that do not have two consecutive ones. More generally, any function accepted by a weighted automaton over the unary alphabet over the semiring (which is in fact a ring, and even a field) is constant-recursive.[citation needed]
Other examples
editThe sequences of Jacobsthal numbers, Padovan numbers, Pell numbers, and Perrin numbers[2] are constant-recursive.
Non-examples
editThe factorial sequence is not constant-recursive. More generally, every constant-recursive function is asymptotically bounded by an exponential function (see #Closed-form characterization) and the factorial sequence grows faster than this.
The Catalan sequence is not constant-recursive. This is because the generating function of the Catalan numbers is not a rational function (see #Equivalent definitions).
Equivalent definitions
editIn terms of matrices
editA sequence is constant-recursive of order less than or equal to if and only if it can be written as
where is a vector, is a matrix, and is a vector, where the elements come from the same domain (integers, rational numbers, algebraic numbers, real numbers, or complex numbers) as the original sequence. Specifically, can be taken to be the first values of the sequence, the linear transformation that computes from , and the vector .[11]
In terms of non-homogeneous linear recurrences
edit| Non-homogeneous | Homogeneous |
|---|---|
A non-homogeneous linear recurrence is an equation of the form
where is an additional constant. Any sequence satisfying a non-homogeneous linear recurrence is constant-recursive. This is because subtracting the equation for from the equation for yields a homogeneous recurrence for , from which we can solve for to obtain[citation needed]
In terms of generating functions
editA sequence is constant-recursive precisely when its generating function
is a rational function , where and are polynomials and .[3] Moreover, the order of the sequence is the minimum such that it has such a form with and .[12]
The denominator is the polynomial obtained from the auxiliary polynomial by reversing the order of the coefficients, and the numerator is determined by the initial values of the sequence:[13][14]
where
It follows from the above that the denominator must be a polynomial not divisible by (and in particular nonzero).
In terms of sequence spaces
editA sequence is constant-recursive if and only if the set of sequences
is contained in a sequence space (vector space of sequences) whose dimension is finite. That is, is contained in a finite-dimensional subspace of closed under the left-shift operator.[16][17]
This characterization is because the order- linear recurrence relation can be understood as a proof of linear dependence between the sequences for . An extension of this argument shows that the order of the sequence is equal to the dimension of the sequence space generated by for all .[18][17]
Closed-form characterization
editConstant-recursive sequences admit the following unique closed form characterization using exponential polynomials: every constant-recursive sequence can be written in the form
for all , where
- The term is a sequence which is zero for all (where is the order of the sequence);
- The terms are complex polynomials; and
- The terms are distinct complex constants.[19][3]
This characterization is exact: every sequence of complex numbers that can be written in the above form is constant-recursive.[20]
For example, the Fibonacci number is written in this form using Binet's formula:[21]
where is the golden ratio and . These are the roots of the equation . In this case, , for all , are both constant polynomials, , and .
The term is only needed when ; if then it corrects for the fact that some initial values may be exceptions to the general recurrence. In particular, for all .[citation needed]
The complex numbers are the roots of the characteristic polynomial of the recurrence:
whose coefficients are the same as those of the recurrence.[22] We call the characteristic roots of the recurrence. If the sequence consists of integers or rational numbers, the roots will be algebraic numbers. If the roots are all distinct, then the polynomials are all constants, which can be determined from the initial values of the sequence. If the roots of the characteristic polynomial are not distinct, and is a root of multiplicity , then in the formula has degree . For instance, if the characteristic polynomial factors as , with the same root r occurring three times, then the th term is of the form [23][24]
Closure properties
editExamples
editThe sum of two constant-recursive sequences is also constant-recursive.[25][26] For example, the sum of and is ( ), which satisfies the recurrence . The new recurrence can be found by adding the generating functions for each sequence.
Similarly, the product of two constant-recursive sequences is constant-recursive.[25] For example, the product of and is ( ), which satisfies the recurrence .
The left-shift sequence and the right-shift sequence (with ) are constant-recursive because they satisfy the same recurrence relation. For example, because is constant-recursive, so is .
List of operations
editIn general, constant-recursive sequences are closed under the following operations, where denote constant-recursive sequences, are their generating functions, and are their orders, respectively.[27]
| Operation | Definition | Requirement | Generating function equivalent | Order |
|---|---|---|---|---|
| Term-wise sum | — | [25] | ||
| Term-wise product | — | [28][29] | [11][25] | |
| Cauchy product | — | [27] | ||
| Left shift | — | [27] | ||
| Right shift | — | [27] | ||
| Cauchy inverse | [27] | |||
| Kleene star | [27] |
The closure under term-wise addition and multiplication follows from the closed-form characterization in terms of exponential polynomials. The closure under Cauchy product follows from the generating function characterization.[27] The requirement for Cauchy inverse is necessary for the case of integer sequences, but can be replaced by if the sequence is over any field (rational, algebraic, real, or complex numbers).[27]
Behavior
editZeros
editDespite satisfying a simple local formula, a constant-recursive sequence can exhibit complicated global behavior. Define a zero of a constant-recursive sequence to be a nonnegative integer such that . The Skolem–Mahler–Lech theorem states that the zeros of the sequence are eventually repeating: there exists constants and such that for all , if and only if . This result holds for a constant-recursive sequence over the complex numbers, or more generally, over any field of characteristic zero.[30]
Decision problems
editThe pattern of zeros in a constant-recursive sequence can also be investigated from the perspective of computability theory. To do so, the description of the sequence must be given a finite description; this can be done if the sequence is over the integers or rational numbers, or even over the algebraic numbers.[11] Given such an encoding for sequences , the following problems can be studied:
| Problem | Description | Status[11][31] |
|---|---|---|
| Existence of a zero (Skolem problem) | On input , is for some ? | Open |
| Infinitely many zeros | On input , is for infinitely many ? | Decidable |
| Eventually all zero | On input , is for all sufficiently large ? | Decidable |
| Positivity | On input , is for all ? | Open |
| Eventual positivity | On input , is for all sufficiently large ? | Open |
Because the square of a constant-recursive sequence is still constant-recursive (see closure properties), the existence-of-a-zero problem in the table above reduces to positivity, and infinitely-many-zeros reduces to eventual positivity. Other problems also reduce to those in the above table: for example, whether for some reduces to existence-of-a-zero for the sequence . As a second example, for sequences in the real numbers, weak positivity (is for all ?) reduces to positivity of the sequence (because the answer must be negated, this is a Turing reduction).
The Skolem-Mahler-Lech theorem would provide answers to some of these questions, except that its proof is non-constructive. It states that for all , the zeros are repeating; however, the value of is not known to be computable, so this does not lead to a solution to the existence-of-a-zero problem.[11] On the other hand, the exact pattern which repeats after is computable.[11][32] This is why the infinitely-many-zeros problem is decidable: just determine if the infinitely-repeating pattern is empty.
Decidability results are known when the order of a sequence is restricted to be small. For example, the Skolem problem is decidable for algebraic sequences of order up to 4.[33][34][35] It is also known to be decidable for reversible integer sequences up to order 7, that is, sequences that may be continued backwards in the integers.[31]
Decidability results are also known under the assumption of certain unproven conjectures in number theory. For example, decidability is known for rational sequences of order up to 5 subject to the Skolem conjecture (also known as the exponential local-global principle). Decidability is also known for all simple rational sequences (those with simple characteristic polynomial) subject to the Skolem conjecture and the weak p-adic Schanuel conjecture.[36]
Degeneracy
editLet be the characteristic roots of a constant recursive sequence . We say that the sequence is degenerate if any ratio is a root of unity, for . It is often easier to study non-degenerate sequences, in a certain sense one can reduce to this using the following theorem: if has order and is contained in a number field of degree over , then there is a constant
such that for some each subsequence is either identically zero or non-degenerate.[37]
Generalizations
editA D-finite or holonomic sequence is a natural generalization where the coefficients of the recurrence are allowed to be polynomial functions of rather than constants.[38]
A -regular sequence satisfies a linear recurrences with constant coefficients, but the recurrences take a different form. Rather than being a linear combination of for some integers that are close to , each term in a -regular sequence is a linear combination of for some integers whose base- representations are close to that of .[39] Constant-recursive sequences can be thought of as -regular sequences, where the base-1 representation of consists of copies of the digit .[citation needed]
Notes
edit- ^ Kauers & Paule 2010, p. 63.
- ^ a b c Kauers & Paule 2010, p. 70.
- ^ a b c Stanley 2011, p. 464.
- ^ Kauers & Paule 2010, p. 66.
- ^ Halava, Vesa; Harju, Tero; Hirvensalo, Mika; Karhumäki, Juhani (2005). "Skolem's Problem – On the Border between Decidability and Undecidability". p. 1. CiteSeerX 10.1.1.155.2606.
- ^ "Index to OEIS: Section Rec - OeisWiki". oeis.org. Retrieved 2024-04-18.
- ^ Boyadzhiev, Boyad (2012). "Close Encounters with the Stirling Numbers of the Second Kind" (PDF). Math. Mag. 85 (4): 252–266. arXiv:1806.09468. doi:10.4169/math.mag.85.4.252. S2CID 115176876.
- ^ Riordan, John (1964). "Inverse Relations and Combinatorial Identities". The American Mathematical Monthly. 71 (5): 485–498. doi:10.1080/00029890.1964.11992269. ISSN 0002-9890.
- ^ Jordan, Charles; Jordán, Károly (1965). Calculus of Finite Differences. American Mathematical Soc. pp. 9–11. ISBN 978-0-8284-0033-6. See formula on p.9, top.
- ^ Kauers & Paule 2010, p. 81.
- ^ a b c d e f Ouaknine, Joël; Worrell, James (2012). "Decision problems for linear recurrence sequences". Reachability Problems: 6th International Workshop, RP 2012, Bordeaux, France, September 17–19, 2012, Proceedings. Lecture Notes in Computer Science. Vol. 7550. Heidelberg: Springer-Verlag. pp. 21–28. doi:10.1007/978-3-642-33512-9_3. ISBN 978-3-642-33511-2. MR 3040104..
- ^ Stanley 2011, pp. 464–465.
- ^ Martino, Ivan; Martino, Luca (2013-11-14). "On the variety of linear recurrences and numerical semigroups". Semigroup Forum. 88 (3): 569–574. arXiv:1207.0111. doi:10.1007/s00233-013-9551-2. ISSN 0037-1912. S2CID 119625519.
- ^ Kauers & Paule 2010, p. 74.
- ^ Stanley 2011, pp. 468–469.
- ^ Kauers & Paule 2010, p. 67.
- ^ a b Stanley 2011, p. 465.
- ^ Kauers & Paule 2010, p. 69.
- ^ Brousseau 1971, pp. 28–34, Lesson 5.
- ^ Kauers & Paule 2010, pp. 68–70.
- ^ Brousseau 1971, p. 16, Lesson 3.
- ^ Brousseau 1971, p. 28, Lesson 5.
- ^ Greene, Daniel H.; Knuth, Donald E. (1982). "2.1.1 Constant coefficients – A) Homogeneous equations". Mathematics for the Analysis of Algorithms (2nd ed.). Birkhäuser. p. 17..
- ^ Brousseau 1971, pp. 29–31, Lesson 5.
- ^ a b c d Kauers & Paule 2010, p. 71.
- ^ Brousseau 1971, p. 37, Lesson 6.
- ^ a b c d e f g h Stanley 2011, pp. 471.
- ^ Pohlen, Timo (2009). "The Hadamard product and universal power series" (PDF). University of Trier (Doctoral Dissertation): 36–37.
- ^ See Hadamard product (series) and Parseval's theorem.
- ^ Lech, C. (1953). "A Note on Recurring Series". Arkiv för Matematik. 2 (5): 417–421. Bibcode:1953ArM.....2..417L. doi:10.1007/bf02590997.
- ^ a b Lipton, Richard; Luca, Florian; Nieuwveld, Joris; Ouaknine, Joël; Purser, David; Worrell, James (2022-08-04). "On the Skolem Problem and the Skolem Conjecture". Proceedings of the 37th Annual ACM/IEEE Symposium on Logic in Computer Science. LICS '22. New York, NY, USA: Association for Computing Machinery. pp. 1–9. doi:10.1145/3531130.3533328. ISBN 978-1-4503-9351-5.
- ^ Berstel, Jean; Mignotte, Maurice (1976). "Deux propriétés décidables des suites récurrentes linéaires". Bulletin de la Société Mathématique de France (in French). 104: 175–184. doi:10.24033/bsmf.1823.
- ^ Vereshchagin, N. K. (1985-08-01). "Occurrence of zero in a linear recursive sequence". Mathematical Notes of the Academy of Sciences of the USSR. 38 (2): 609–615. doi:10.1007/BF01156238. ISSN 1573-8876.
- ^ Tijdeman, R.; Mignotte, M.; Shorey, T. N. (1984). "The distance between terms of an algebraic recurrence sequence". Journal für die reine und angewandte Mathematik. 349: 63–76. ISSN 0075-4102.
- ^ Bacik, Piotr (2024-09-02). "Completing the picture for the Skolem Problem on order-4 linear recurrence sequences". arXiv:2409.01221 [cs.FL].
- ^ Bilu, Yuri; Luca, Florian; Nieuwveld, Joris; Ouaknine, Joël; Purser, David; Worrell, James (2022-04-28). "Skolem Meets Schanuel". arXiv:2204.13417 [cs.LO].
- ^ Everest, Graham, ed. (2003). Recurrence sequences. Mathematical surveys and monographs. Providence, RI: American Mathematical Society. p. 5. ISBN 978-0-8218-3387-2.
- ^ Stanley, Richard P (1980). "Differentiably finite power series". European Journal of Combinatorics. 1 (2): 175–188. doi:10.1016/S0195-6698(80)80051-5.
- ^ Allouche, Jean-Paul; Shallit, Jeffrey (1992). "The ring of k-regular sequences". Theoretical Computer Science. 98 (2): 163–197. doi:10.1016/0304-3975(92)90001-V.
References
edit- Brousseau, Alfred (1971). Linear Recursion and Fibonacci Sequences. Fibonacci Association.
- Kauers, Manuel; Paule, Peter (2010). The Concrete Tetrahedron: Symbolic Sums, Recurrence Equations, Generating Functions, Asymptotic Estimates. Springer Vienna. p. 66. ISBN 978-3-7091-0444-6.
- Stanley, Richard P. (2011). Enumerative Combinatorics (PDF). Vol. 1 (2 ed.). Cambridge studies in advanced mathematics.
External links
edit- "OEIS Index Rec". OEIS index to a few thousand examples of linear recurrences, sorted by order (number of terms) and signature (vector of values of the constant coefficients)








