Inverse-square law

In science, an inverse-square law is any scientific law stating that the observed "intensity" of a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. The fundamental cause for this can be understood as geometric dilution corresponding to point-source radiation into three-dimensional space.

Radar energy expands during both the signal transmission and the reflected return, so the inverse square for both paths means that the radar will receive energy according to the inverse fourth power of the range.

To prevent dilution of energy while propagating a signal, certain methods can be used such as a waveguide, which acts like a canal does for water, or how a gun barrel restricts hot gas expansion to one dimension in order to prevent loss of energy transfer to a bullet.

Formula

In mathematical notation the inverse square law can be expressed as an intensity (I) varying as a function of distance (d) from some centre. The intensity is proportional (see ∝) to the reciprocal of the square of the distance thus: ${\text{intensity}}\ \propto \ {\frac {1}{{\text{distance}}^{2}}}\,$

It can also be mathematically expressed as : ${\frac {{\text{intensity}}_{1}}{{\text{intensity}}_{2}}}={\frac {{\text{distance}}_{2}^{2}}{{\text{distance}}_{1}^{2}}}$

or as the formulation of a constant quantity: ${\text{intensity}}_{1}\times {\text{distance}}_{1}^{2}={\text{intensity}}_{2}\times {\text{distance}}_{2}^{2}$

The divergence of a vector field which is the resultant of radial inverse-square law fields with respect to one or more sources is proportional to the strength of the local sources, and hence zero outside sources. Newton's law of universal gravitation follows an inverse-square law, as do the effects of electric, light, sound, and radiation phenomena.

Justification

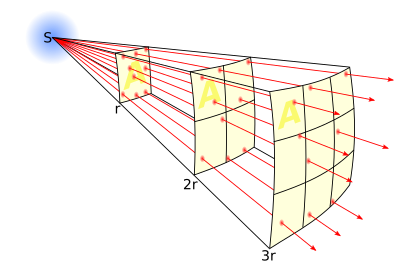
The inverse-square law generally applies when some force, energy, or other conserved quantity is evenly radiated outward from a point source in three-dimensional space. Since the surface area of a sphere (which is 4πr²) is proportional to the square of the radius, as the emitted radiation gets farther from the source, it is spread out over an area that is increasing in proportion to the square of the distance from the source. Hence, the intensity of radiation passing through any unit area (directly facing the point source) is inversely proportional to the square of the distance from the point source. Gauss's law for gravity is similarly applicable, and can be used with any physical quantity that acts in accordance with the inverse-square relationship.

Occurrences

Gravitation

Gravitation is the attraction between objects that have mass. Newton's law states:

The gravitational attraction force between two point masses is directly proportional to the product of their masses and inversely proportional to the square of their separation distance. The force is always attractive and acts along the line joining them.^{[citation needed]}

If the distribution of matter in each body is spherically symmetric, then the objects can be treated as point masses without approximation, as shown in the shell theorem. Otherwise, if we want to calculate the attraction between massive bodies, we need to add all the point-point attraction forces vectorially and the net attraction might not be exact inverse square. However, if the separation between the massive bodies is much larger compared to their sizes, then to a good approximation, it is reasonable to treat the masses as a point mass located at the object's center of mass while calculating the gravitational force.

As the law of gravitation, this law was suggested in 1645 by Ismaël Bullialdus. But Bullialdus did not accept Kepler's second and third laws, nor did he appreciate Christiaan Huygens's solution for circular motion (motion in a straight line pulled aside by the central force). Indeed, Bullialdus maintained the sun's force was attractive at aphelion and repulsive at perihelion. Robert Hooke and Giovanni Alfonso Borelli both expounded gravitation in 1666 as an attractive force.^[1] Hooke's lecture "On gravity" was at the Royal Society, in London, on 21 March.^[2] Borelli's "Theory of the Planets" was published later in 1666.^[3] Hooke's 1670 Gresham lecture explained that gravitation applied to "all celestiall bodys" and added the principles that the gravitating power decreases with distance and that in the absence of any such power bodies move in straight lines. By 1679, Hooke thought gravitation had inverse square dependence and communicated this in a letter to Isaac Newton:^[4] my supposition is that the attraction always is in duplicate proportion to the distance from the center reciprocall.^[5]

Hooke remained bitter about Newton claiming the invention of this principle, even though Newton's 1686 Principia acknowledged that Hooke, along with Wren and Halley, had separately appreciated the inverse square law in the solar system,^[6] as well as giving some credit to Bullialdus.^[7]

Electrostatics

The force of attraction or repulsion between two electrically charged particles, in addition to being directly proportional to the product of the electric charges, is inversely proportional to the square of the distance between them; this is known as Coulomb's law. The deviation of the exponent from 2 is less than one part in 10¹⁵.^[8]

$F=k_{\text{e}}{\frac {q_{1}q_{2}}{r^{2}}}$

Light and other electromagnetic radiation

The intensity (or illuminance or irradiance) of light or other linear waves radiating from a point source (energy per unit of area perpendicular to the source) is inversely proportional to the square of the distance from the source, so an object (of the same size) twice as far away receives only one-quarter the energy (in the same time period).

More generally, the irradiance, i.e., the intensity (or power per unit area in the direction of propagation), of a spherical wavefront varies inversely with the square of the distance from the source (assuming there are no losses caused by absorption or scattering).

For example, the intensity of radiation from the Sun is 9126 watts per square meter at the distance of Mercury (0.387 AU); but only 1367 watts per square meter at the distance of Earth (1 AU)—an approximate threefold increase in distance results in an approximate ninefold decrease in intensity of radiation.

For non-isotropic radiators such as parabolic antennas, headlights, and lasers, the effective origin is located far behind the beam aperture. If you are close to the origin, you don't have to go far to double the radius, so the signal drops quickly. When you are far from the origin and still have a strong signal, like with a laser, you have to travel very far to double the radius and reduce the signal. This means you have a stronger signal or have antenna gain in the direction of the narrow beam relative to a wide beam in all directions of an isotropic antenna.

In photography and stage lighting, the inverse-square law is used to determine the “fall off” or the difference in illumination on a subject as it moves closer to or further from the light source. For quick approximations, it is enough to remember that doubling the distance reduces illumination to one quarter;^[9] or similarly, to halve the illumination increase the distance by a factor of 1.4 (the square root of 2), and to double illumination, reduce the distance to 0.7 (square root of 1/2). When the illuminant is not a point source, the inverse square rule is often still a useful approximation; when the size of the light source is less than one-fifth of the distance to the subject, the calculation error is less than 1%.^[10]

The fractional reduction in electromagnetic fluence (Φ) for indirectly ionizing radiation with increasing distance from a point source can be calculated using the inverse-square law. Since emissions from a point source have radial directions, they intercept at a perpendicular incidence. The area of such a shell is 4πr ² where r is the radial distance from the center. The law is particularly important in diagnostic radiography and radiotherapy treatment planning, though this proportionality does not hold in practical situations unless source dimensions are much smaller than the distance. As stated in Fourier theory of heat “as the point source is magnification by distances, its radiation is dilute proportional to the sin of the angle, of the increasing circumference arc from the point of origin”.

Example

Let P be the total power radiated from a point source (for example, an omnidirectional isotropic radiator). At large distances from the source (compared to the size of the source), this power is distributed over larger and larger spherical surfaces as the distance from the source increases. Since the surface area of a sphere of radius r is A = 4πr², the intensity I (power per unit area) of radiation at distance r is $I={\frac {P}{A}}={\frac {P}{4\pi r^{2}}}.\,$

The energy or intensity decreases (divided by 4) as the distance r is doubled; if measured in dB would decrease by 6.02 dB per doubling of distance. When referring to measurements of power quantities, a ratio can be expressed as a level in decibels by evaluating ten times the base-10 logarithm of the ratio of the measured quantity to the reference value.

Sound in a gas

In acoustics, the sound pressure of a spherical wavefront radiating from a point source decreases by 50% as the distance r is doubled; measured in dB, the decrease is still 6.02 dB, since dB represents an intensity ratio. The pressure ratio (as opposed to power ratio) is not inverse-square, but is inverse-proportional (inverse distance law):

$p\ \propto \ {\frac {1}{r}}\,$

The same is true for the component of particle velocity $v\,$ that is in-phase with the instantaneous sound pressure $p\,$ :

$v\ \propto {\frac {1}{r}}\ \,$

In the near field is a quadrature component of the particle velocity that is 90° out of phase with the sound pressure and does not contribute to the time-averaged energy or the intensity of the sound. The sound intensity is the product of the RMS sound pressure and the in-phase component of the RMS particle velocity, both of which are inverse-proportional. Accordingly, the intensity follows an inverse-square behaviour:

$I\ =\ pv\ \propto \ {\frac {1}{r^{2}}}.\,$

Field theory interpretation

For an irrotational vector field in three-dimensional space, the inverse-square law corresponds to the property that the divergence is zero outside the source. This can be generalized to higher dimensions. Generally, for an irrotational vector field in n-dimensional Euclidean space, the intensity "I" of the vector field falls off with the distance "r" following the inverse (n − 1)^th power law

$I\propto {\frac {1}{r^{n-1}}},$

given that the space outside the source is divergence free. ^{[citation needed]}

Non-Euclidean implications

The inverse-square law, fundamental in Euclidean spaces, also applies to non-Euclidean geometries, including hyperbolic space. The curvature present in these spaces alters physical laws, influencing a variety of fields such as cosmology, general relativity, and string theory.^[11]

John D. Barrow, in his 2020 paper "Non-Euclidean Newtonian Cosmology," expands on the behavior of force (F) and potential (Φ) within hyperbolic 3-space (H3). He explains that F and Φ obey the relationships F ∝ 1 / R² sinh²(r/R) and Φ ∝ coth(r/R), where R represents the curvature radius and r represents the distance from the focal point.

The concept of spatial dimensionality, first proposed by Immanuel Kant, remains a topic of debate concerning the inverse-square law.^[12] Dimitria Electra Gatzia and Rex D. Ramsier, in their 2021 paper, contend that the inverse-square law is more closely related to force distribution symmetry than to the dimensionality of space.

In the context of non-Euclidean geometries and general relativity, deviations from the inverse-square law do not arise from the law itself but rather from the assumption that the force between two bodies is instantaneous, which contradicts special relativity. General relativity reinterprets gravity as the curvature of spacetime, leading particles to move along geodesics in this curved spacetime.^[13]

History

John Dumbleton of the 14th-century Oxford Calculators, was one of the first to express functional relationships in graphical form. He gave a proof of the mean speed theorem stating that "the latitude of a uniformly difform movement corresponds to the degree of the midpoint" and used this method to study the quantitative decrease in intensity of illumination in his Summa logicæ et philosophiæ naturalis (ca. 1349), stating that it was not linearly proportional to the distance, but was unable to expose the Inverse-square law.^[14]

German astronomer Johannes Kepler discussed the inverse-square law and how it affects the intensity of light.

In proposition 9 of Book 1 in his book Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur (1604), the astronomer Johannes Kepler argued that the spreading of light from a point source obeys an inverse square law:^[15]^[16]

Sicut se habent spharicae superificies, quibus origo lucis pro centro est, amplior ad angustiorem: ita se habet fortitudo seu densitas lucis radiorum in angustiori, ad illamin in laxiori sphaerica, hoc est, conversim. Nam per 6. 7. tantundem lucis est in angustiori sphaerica superficie, quantum in fusiore, tanto ergo illie stipatior & densior quam hic.

Just as [the ratio of] spherical surfaces, for which the source of light is the center, [is] from the wider to the narrower, so the density or fortitude of the rays of light in the narrower [space], towards the more spacious spherical surfaces, that is, inversely. For according to [propositions] 6 & 7, there is as much light in the narrower spherical surface, as in the wider, thus it is as much more compressed and dense here than there.

In 1645, in his book Astronomia Philolaica ..., the French astronomer Ismaël Bullialdus (1605–1694) refuted Johannes Kepler's suggestion that "gravity"^[17] weakens as the inverse of the distance; instead, Bullialdus argued, "gravity" weakens as the inverse square of the distance:^[18]^[19]

Virtus autem illa, qua Sol prehendit seu harpagat planetas, corporalis quae ipsi pro manibus est, lineis rectis in omnem mundi amplitudinem emissa quasi species solis cum illius corpore rotatur: cum ergo sit corporalis imminuitur, & extenuatur in maiori spatio & intervallo, ratio autem huius imminutionis eadem est, ac luminus, in ratione nempe dupla intervallorum, sed eversa.

As for the power by which the Sun seizes or holds the planets, and which, being corporeal, functions in the manner of hands, it is emitted in straight lines throughout the whole extent of the world, and like the species of the Sun, it turns with the body of the Sun; now, seeing that it is corporeal, it becomes weaker and attenuated at a greater distance or interval, and the ratio of its decrease in strength is the same as in the case of light, namely, the duplicate proportion, but inversely, of the distances [that is, 1/d²].

In England, the Anglican bishop Seth Ward (1617–1689) publicized the ideas of Bullialdus in his critique In Ismaelis Bullialdi astronomiae philolaicae fundamenta inquisitio brevis (1653) and publicized the planetary astronomy of Kepler in his book Astronomia geometrica (1656).

In 1663–1664, the English scientist Robert Hooke was writing his book Micrographia (1666) in which he discussed, among other things, the relation between the height of the atmosphere and the barometric pressure at the surface. Since the atmosphere surrounds the Earth, which itself is a sphere, the volume of atmosphere bearing on any unit area of the Earth's surface is a truncated cone (which extends from the Earth's center to the vacuum of space; obviously only the section of the cone from the Earth's surface to space bears on the Earth's surface). Although the volume of a cone is proportional to the cube of its height, Hooke argued that the air's pressure at the Earth's surface is instead proportional to the height of the atmosphere because gravity diminishes with altitude. Although Hooke did not explicitly state so, the relation that he proposed would be true only if gravity decreases as the inverse square of the distance from the Earth's center.^[20]^[21]

References

This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 22 January 2022.

^ Hooke's gravitation was also not yet universal, though it approached universality more closely than previous hypotheses. See page 239 in: Taton, René; Wilson, Curtis; Hoskin, Michael A., eds. (2009). "The Newtonian achievement in astronomy". General history of astronomy. Vol. 2 Pt. A: Planetary astronomy from the Renaissance to the rise of astrophysics Tycho Brahe to Newton (1. ed.). Cambridge: Cambridge University Press. pp. 233–274. ISBN 978-0-521-54205-0.
^ Birch, Thomas (1756). The History of the Royal Society of London. Vol. 2. pp. 68–73.; see especially pages 70–72.
^ Borelli, Giovanni Alfonso (1666). Theoricae mediceorum planetarum ex causis physicis deductae [Theory [of the motion] of the Medicean planets [i.e., moons of Jupiter] deduced from physical causes] (in Latin). Ex typographia S.M.D. Bibcode:1666tmpe.book.....B.
^ Koyré, Alexandre (1952). "An Unpublished Letter of Robert Hooke to Isaac Newton". Isis. 43 (4): 312–337. doi:10.1086/348155. ISSN 0021-1753. JSTOR 227384. PMID 13010921. S2CID 41626961.
^ Hooke's letter to Newton of 6 January 1680 (Koyré 1952:332).
^ Newton acknowledged Wren, Hooke and Halley in this connection in the Scholium to Proposition 4 in Book 1 (in all editions): See for example: Newton, Isaac (1729). The Mathematical Principles of Natural Philosophy. B. Motte. p. 66.
^ In a letter to Edmund Halley dated 20 June 1686, Newton wrote: "Bullialdus wrote that all force respecting ye Sun as its center & depending on matter must be reciprocally in a duplicate ratio of ye distance from ye center." See: Cohen, I. Bernard; Smith, George E. (2002). The Cambridge Companion to Newton. Cambridge University Press. p. 204. ISBN 978-0-521-65696-2.
^ Williams, E. R.; Faller, J. E.; Hill, H. A. (1971). "New Experimental Test of Coulomb's Law: A Laboratory Upper Limit on the Photon Rest Mass". Physical Review Letters. 26 (12): 721–724. Bibcode:1971PhRvL..26..721W. doi:10.1103/PhysRevLett.26.721. ISSN 0031-9007.
^ Millerson, Gerald (1999). Lighting for TV and Film. CRC Press. p. 27. ISBN 978-1-136-05522-5.
^ Ryder, Alexander D. (1997). The Light Measurement Handbook (PDF). International Light. p. 26. ISBN 978-0-96-583569-5.
^ Barrow, John D (2020). "Non-Euclidean Newtonian cosmology". Classical and Quantum Gravity. 37 (12): 125007. arXiv:2002.10155. Bibcode:2020CQGra..37l5007B. doi:10.1088/1361-6382/ab8437. ISSN 0264-9381.
^ Gatzia, Dimitria Electra; Ramsier, Rex D. (2021). "Dimensionality, symmetry and the Inverse Square Law". Notes and Records: The Royal Society Journal of the History of Science. 75 (3): 333–348. doi:10.1098/rsnr.2019.0044. ISSN 0035-9149.
^ Guth, Alan (2018). "Introduction to Non-Euclidean General Relativity" (PDF). MIT OpenCourseWare. Retrieved 30 July 2023.
^ Freely, John (2012). Before Galileo: The Birth of Modern Science in Medieval Europe. Overlook Duckworth. ISBN 978-0-71-564536-9.
^ Kepler, Johannes (1604). Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur (in Latin). Apud Claudium Marnium & haeredes Ioannis Aubrii. p. 10.
^ Translation of the Latin quote from Kepler's Ad Vitellionem paralipomena is from: Gal, Ofer; Chen-Morris, Raz (2005). "The Archaeology of the Inverse Square Law: (1) Metaphysical Images and Mathematical Practices". History of Science. 43 (4): 391–414. Bibcode:2005HisSc..43..391G. doi:10.1177/007327530504300402. ; see especially p. 397.
^ Note: Both Kepler and William Gilbert had nearly anticipated the modern conception of gravity, lacking only the inverse-square law in their description of "gravitas". On page 4 of chapter 1, Introductio, of Astronomia Nova, Kepler sets out his description as follows: "The true theory of gravity is founded on the following axioms: Every corporeal substance, so far forth as it is corporeal, has a natural fitness for resting in every place where it may be situated by itself beyond the sphere of influence of a body cognate with it. Gravity is a mutual affection between cognate bodies towards union or conjunction (similar in kind to the magnetic virtue), so that the earth attracts a stone much rather than the stone seeks the earth. ... If two stones were placed in any part of the world near each other, and beyond the sphere of influence of a third cognate body, these stones, like two magnetic needles, would come together in the intermediate point, each approaching the other by a space proportional to the comparative mass of the other. If the moon and earth were not retained in their orbits by their animate force or some other equivalent, the earth would mount to the moon by a fifty-fourth part of their distance, and the moon fall towards the earth through the other fifty-three parts, and they would there meet, assuming, however, that the substance of both is of the same density." Notice that in saying "the earth attracts a stone much rather than the stone seeks the earth" Kepler is breaking away from the Aristotelian tradition that objects seek to be in their natural place, that a stone seeks to be with the earth.
^ Boulliau, Ismael (1645). Astronomia Philolaica (in Latin). Simeon Piget. p. 23. Bibcode:1645ibap.book.....B. doi:10.3931/e-rara-549.
^ Translation of the Latin quote from Bullialdus' 'Astronomia Philolaica' … is from: O'Connor, John J.; Robertson, Edmund F. (2006). "Ismael Boulliau". The MacTutor History of Mathematics Archive. University of Saint Andrews.
^ Gal & Chen-Morris 2005, pp. 391–392
^ Hooke, Robert (1665). Micrographia. Science Heritage. p. 227. ISBN 978-0-940095-07-6. I say a Cylinder, not a piece of a Cone, because, as I may elsewhere shew in the Explication of Gravity, that triplicate proportion of the shels of a Sphere, to their respective diameters, I suppose to be removed in this case by the decrease of the power of Gravity.

External links

[1] Hooke's gravitation was also not yet universal, though it approached universality more closely than previous hypotheses. See page 239 in: Taton, René; Wilson, Curtis; Hoskin, Michael A., eds. (2009). "The Newtonian achievement in astronomy". General history of astronomy. Vol. 2 Pt. A: Planetary astronomy from the Renaissance to the rise of astrophysics Tycho Brahe to Newton (1. ed.). Cambridge: Cambridge University Press. pp. 233–274. ISBN 978-0-521-54205-0.

[2] Birch, Thomas (1756). The History of the Royal Society of London. Vol. 2. pp. 68–73.; see especially pages 70–72.

[3] Borelli, Giovanni Alfonso (1666). Theoricae mediceorum planetarum ex causis physicis deductae [Theory [of the motion] of the Medicean planets [i.e., moons of Jupiter] deduced from physical causes] (in Latin). Ex typographia S.M.D. Bibcode:1666tmpe.book.....B.

[Hooke1680-4] Koyré, Alexandre (1952). "An Unpublished Letter of Robert Hooke to Isaac Newton". Isis. 43 (4): 312–337. doi:10.1086/348155. ISSN 0021-1753. JSTOR 227384. PMID 13010921. S2CID 41626961.

[5] Hooke's letter to Newton of 6 January 1680 (Koyré 1952:332).

[6] Newton acknowledged Wren, Hooke and Halley in this connection in the Scholium to Proposition 4 in Book 1 (in all editions): See for example: Newton, Isaac (1729). The Mathematical Principles of Natural Philosophy. B. Motte. p. 66.

[7] In a letter to Edmund Halley dated 20 June 1686, Newton wrote: "Bullialdus wrote that all force respecting ye Sun as its center & depending on matter must be reciprocally in a duplicate ratio of ye distance from ye center." See: Cohen, I. Bernard; Smith, George E. (2002). The Cambridge Companion to Newton. Cambridge University Press. p. 204. ISBN 978-0-521-65696-2.

[8] Williams, E. R.; Faller, J. E.; Hill, H. A. (1971). "New Experimental Test of Coulomb's Law: A Laboratory Upper Limit on the Photon Rest Mass". Physical Review Letters. 26 (12): 721–724. Bibcode:1971PhRvL..26..721W. doi:10.1103/PhysRevLett.26.721. ISSN 0031-9007.

[9] Millerson, Gerald (1999). Lighting for TV and Film. CRC Press. p. 27. ISBN 978-1-136-05522-5.

[10] Ryder, Alexander D. (1997). The Light Measurement Handbook (PDF). International Light. p. 26. ISBN 978-0-96-583569-5.

[11] Barrow, John D (2020). "Non-Euclidean Newtonian cosmology". Classical and Quantum Gravity. 37 (12): 125007. arXiv:2002.10155. Bibcode:2020CQGra..37l5007B. doi:10.1088/1361-6382/ab8437. ISSN 0264-9381.

[12] Gatzia, Dimitria Electra; Ramsier, Rex D. (2021). "Dimensionality, symmetry and the Inverse Square Law". Notes and Records: The Royal Society Journal of the History of Science. 75 (3): 333–348. doi:10.1098/rsnr.2019.0044. ISSN 0035-9149.

[13] Guth, Alan (2018). "Introduction to Non-Euclidean General Relativity" (PDF). MIT OpenCourseWare. Retrieved 30 July 2023.

[14] Freely, John (2012). Before Galileo: The Birth of Modern Science in Medieval Europe. Overlook Duckworth. ISBN 978-0-71-564536-9.

[15] Kepler, Johannes (1604). Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur (in Latin). Apud Claudium Marnium & haeredes Ioannis Aubrii. p. 10.

[16] Translation of the Latin quote from Kepler's Ad Vitellionem paralipomena is from: Gal, Ofer; Chen-Morris, Raz (2005). "The Archaeology of the Inverse Square Law: (1) Metaphysical Images and Mathematical Practices". History of Science. 43 (4): 391–414. Bibcode:2005HisSc..43..391G. doi:10.1177/007327530504300402. ; see especially p. 397.

[17] Note: Both Kepler and William Gilbert had nearly anticipated the modern conception of gravity, lacking only the inverse-square law in their description of "gravitas". On page 4 of chapter 1, Introductio, of Astronomia Nova, Kepler sets out his description as follows: "The true theory of gravity is founded on the following axioms: Every corporeal substance, so far forth as it is corporeal, has a natural fitness for resting in every place where it may be situated by itself beyond the sphere of influence of a body cognate with it. Gravity is a mutual affection between cognate bodies towards union or conjunction (similar in kind to the magnetic virtue), so that the earth attracts a stone much rather than the stone seeks the earth. ... If two stones were placed in any part of the world near each other, and beyond the sphere of influence of a third cognate body, these stones, like two magnetic needles, would come together in the intermediate point, each approaching the other by a space proportional to the comparative mass of the other. If the moon and earth were not retained in their orbits by their animate force or some other equivalent, the earth would mount to the moon by a fifty-fourth part of their distance, and the moon fall towards the earth through the other fifty-three parts, and they would there meet, assuming, however, that the substance of both is of the same density." Notice that in saying "the earth attracts a stone much rather than the stone seeks the earth" Kepler is breaking away from the Aristotelian tradition that objects seek to be in their natural place, that a stone seeks to be with the earth.

[18] Boulliau, Ismael (1645). Astronomia Philolaica (in Latin). Simeon Piget. p. 23. Bibcode:1645ibap.book.....B. doi:10.3931/e-rara-549.

[19] Translation of the Latin quote from Bullialdus' 'Astronomia Philolaica' … is from: O'Connor, John J.; Robertson, Edmund F. (2006). "Ismael Boulliau". The MacTutor History of Mathematics Archive. University of Saint Andrews.

[20] Gal & Chen-Morris 2005, pp. 391–392

[21] Hooke, Robert (1665). Micrographia. Science Heritage. p. 227. ISBN 978-0-940095-07-6. I say a Cylinder, not a piece of a Cone, because, as I may elsewhere shew in the Explication of Gravity, that triplicate proportion of the shels of a Sphere, to their respective diameters, I suppose to be removed in this case by the decrease of the power of Gravity.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]