Gauss–Kuzmin distribution

In mathematics, the Gauss–Kuzmin distribution is a discrete probability distribution that arises as the limit probability distribution of the coefficients in the continued fraction expansion of a random variable uniformly distributed in (0, 1). The distribution is named after Carl Friedrich Gauss, who derived it around 1800, and Rodion Kuzmin, who gave a bound on the rate of convergence in 1929. It is given by the probability mass function

Gauss–Kuzmin

Probability mass function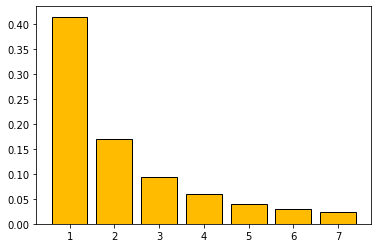
Cumulative distribution function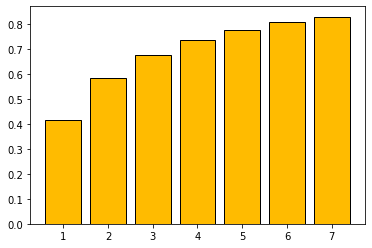
Parameters	(none)
Support	$k\in \{1,2,\ldots \}$
PMF	$-\log _{2}\left[1-{\frac {1}{(k+1)^{2}}}\right]$
CDF	$1-\log _{2}\left({\frac {k+2}{k+1}}\right)$
Mean	$+\infty$
Median	$2\,$
Mode	$1\,$
Variance	$+\infty$
Skewness	(not defined)
Excess kurtosis	(not defined)
Entropy	3.432527514776...

$p(k)=-\log _{2}\left(1-{\frac {1}{(1+k)^{2}}}\right)~.$

Gauss–Kuzmin theorem

Let

$x={\cfrac {1}{k_{1}+{\cfrac {1}{k_{2}+\cdots }}}}$

be the continued fraction expansion of a random number x uniformly distributed in (0, 1). Then

$\lim _{n\to \infty }\mathbb {P} \left\{k_{n}=k\right\}=-\log _{2}\left(1-{\frac {1}{(k+1)^{2}}}\right)~.$

Equivalently, let

$x_{n}={\cfrac {1}{k_{n+1}+{\cfrac {1}{k_{n+2}+\cdots }}}}~;$

then

$\Delta _{n}(s)=\mathbb {P} \left\{x_{n}\leq s\right\}-\log _{2}(1+s)$

tends to zero as n tends to infinity.

Rate of convergence

In 1928, Kuzmin gave the bound

$|\Delta _{n}(s)|\leq C\exp(-\alpha {\sqrt {n}})~.$

In 1929, Paul Lévy improved it to

$|\Delta _{n}(s)|\leq C\,0.7^{n}~.$

Later, Eduard Wirsing showed that, for λ = 0.30366... (the Gauss–Kuzmin–Wirsing constant), the limit

$\Psi (s)=\lim _{n\to \infty }{\frac {\Delta _{n}(s)}{(-\lambda )^{n}}}$

exists for every s in [0, 1], and the function Ψ(s) is analytic and satisfies Ψ(0) = Ψ(1) = 0. Further bounds were proved by K. I. Babenko.

See also

• Khinchin's constant
• Lévy's constant