No higher resolution available.
Polarization_change_in_uniaxial_crystal.gif (360 × 244 pixels, file size: 339 KB, MIME type: image/gif, looped, 31 frames)
 | This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Summary
| Description |
English: A wave in a uniaxial crystal will separate in two components, one parallel and one perpendicular to the optic axis, that will accumulating phase at different rates. This can be used to manipulate the polarization state of the wave. |
| Date | |
| Source | https://twitter.com/j_bertolotti/status/1198606136586444801 |
| Author | Jacopo Bertolotti |
| Permission (Reusing this file) |
https://twitter.com/j_bertolotti/status/1030470604418428929 |
Mathematica 11.0 code
\[Theta] = \[Pi]/4;
\[Epsilon]r = FullSimplify@RotationMatrix[\[Theta], {1, 0, 0}].DiagonalMatrix[{\[Epsilon]1, \[Epsilon]1, \[Epsilon]2}].RotationMatrix[-\[Theta], {1, 0, 0}];
eq = Table[
(D[{Ex[x], Ey[x], Ez[x]}, {x, 2}])[[j]] == -(\[Epsilon]r.{Ex[x], Ey[x], Ez[x]})[[j]], {j, 1, 3, 1}];
sol = FullSimplify[DSolveValue[Flatten[{eq, Ex[0] == 0, Ex'[0] == 0, Ey[0] == 0, Ey'[0] == 0, Ez[0] == 1, Ez'[0] == 0}], {Ex[x], Ey[x], Ez[x]}, x] ];
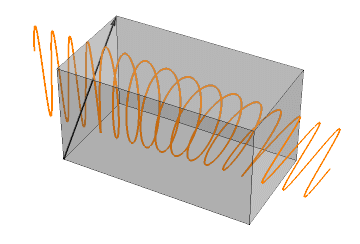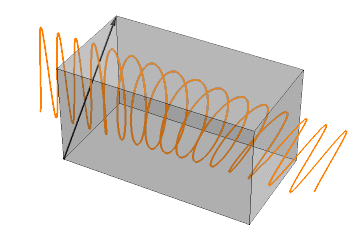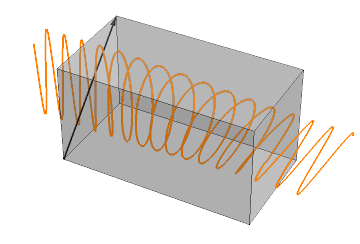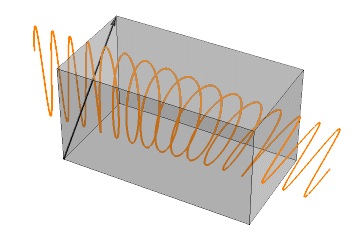
p1 = Table[ Show[
Graphics3D[{Lighting -> "Neutral", Gray, Opacity[0.3], Cuboid[{0, -1, -1}, {62.8, 1, 1}], Opacity[1], Thick, Black, Arrowheads[0.002], Arrow[{{0, -1, -1}, {0, 1, 1}}]}]
,
ParametricPlot3D[Piecewise[{{{x, 0, Cos[x - \[Tau]]} /. {\[Epsilon]1 -> 1, \[Epsilon]2 -> 1.1}, x < 0}, {{x, sol2[[2]], sol2[[3]]} /. {\[Epsilon]1 -> 1, \[Epsilon]2 -> 1.1}, 0 < x < 62.8}, {{x, Cos[x - \[Tau]], 0} /. {\[Epsilon]1 -> 1, \[Epsilon]2 -> 1.1}, x > 62.8}}], {x, -20, 80}, BoxRatios -> {3, 1, 1}, PlotStyle -> {Orange}, PlotPoints -> 50]
, PlotRange -> {{-20, 80}, {-1, 1}, {-1, 1}}, BoxRatios -> {3, 1, 1}, Boxed -> False
]
, {\[Tau], 0, 2 \[Pi], (2 \[Pi])/30}];
ListAnimate[p1]
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
 
|
This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. |
| The person who associated a work with this deed has dedicated the work to the public domain by waiving all of their rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law. You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
|
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 09:30, 25 November 2019 | | 360 × 244 (339 KB) | Berto | User created page with UploadWizard |
File usage
The following page uses this file:
Global file usage
The following other wikis use this file:
- Usage on af.wiki.x.io
- Usage on fa.wiki.x.io
- Usage on fr.wikibooks.org
- Usage on th.wiki.x.io
